Improve the inequality
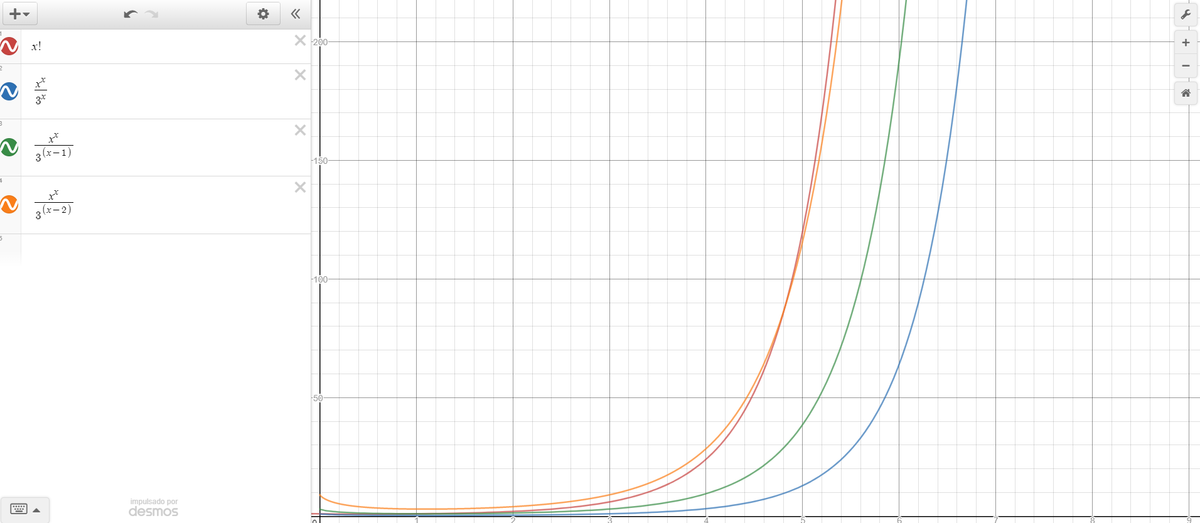
It is a standard exercise in induction to prove that for n ≥ 1 the inequality ( 3 n ) n < n ! holds. While this is an interesting result, if one observes a graph comparing the two functions one notices that this inequality is actually extremely weak in the sense that the difference between n ! and ( 3 n ) n quickly becomes larger and larger as n increases. In some inequalities, this behavior is to be expected but it can also make us think about how to leverage this fact to get a better inequality for large n .
Let a ≥ 1 be an integer. A way to improve the previous inequality is by finding some integer n 0 such that for all n ≥ n 0 the inequality 3 n − a n n < n ! holds. Notice that if we let a = 0 we have the original inequality. To give an example, if we let a = 1 then n 0 = 2 seems to work. The question is, for what values of a can we find a corresponding n 0 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since
ln
(
x
)
is monotonically increasing for
x
>
0
, we have
ln
(
n
!
)
=
r
=
1
∑
n
ln
(
r
)
≥
∫
1
n
ln
(
x
)
d
x
>
n
ln
(
n
/
e
)
.
Exponentiating both sides, we have
n
!
>
(
e
n
)
n
.
Since
(
3
/
e
)
n
→
∞
, as
n
→
∞
, for any
a
, there exists a finite
n
0
, such that
3
n
−
a
>
e
n
for all
n
≥
n
0
. This gives, for all
n
≥
n
0
,
n
!
>
3
n
−
a
n
n
.
In the induction proof for the inequality ( 3 n ) n < n ! one inevitably finds the known expression ( 1 + n 1 ) n and uses the fact that this is between 2 and 3 to conclude. But having more experience, we know that ( 1 + n 1 ) n is related to the famous constant e . In particular, lim n → ∞ ( 1 + n 1 ) n = e so one way of getting a better inequality is finding a stronger way to relate e and ( 3 n ) n . Consider the following: Let u = n − 1 . Then
( 3 n ) n = ( 3 u + 1 ) u + 1 = 3 u + 1 1 ( u + 1 ) ( u + 1 ) = 3 u + 1 1 k = 0 ∑ u + 1 ( k u + 1 ) u k ≤ 3 u + 1 1 k = 0 ∑ u + 1 k ! ( u + 1 ) ! u k < 3 u + 1 ( u + 1 ) ! k = 0 ∑ ∞ k ! u k = 3 u + 1 ( u + 1 ) ! e u = 3 n n ! e n − 1
This implies
( 3 n ) n n ! > 3 n n ! e n − 1 n ! = e n − 1 3 n
And notice that this last expression goes to infinity so to pick our n 0 simply choose one such that e n 0 − 1 3 n 0 > 3 a and then that will imply that for n ≥ n 0 , ( 3 n ) n n ! > 3 a ⟹ n ! > 3 a ( 3 n ) n = 3 n − a n n
And with just this, we were able to obtain some very nice inequalities: