Improved Relativistic Mass and Momentum Problem

Classical Mechanics Level 5

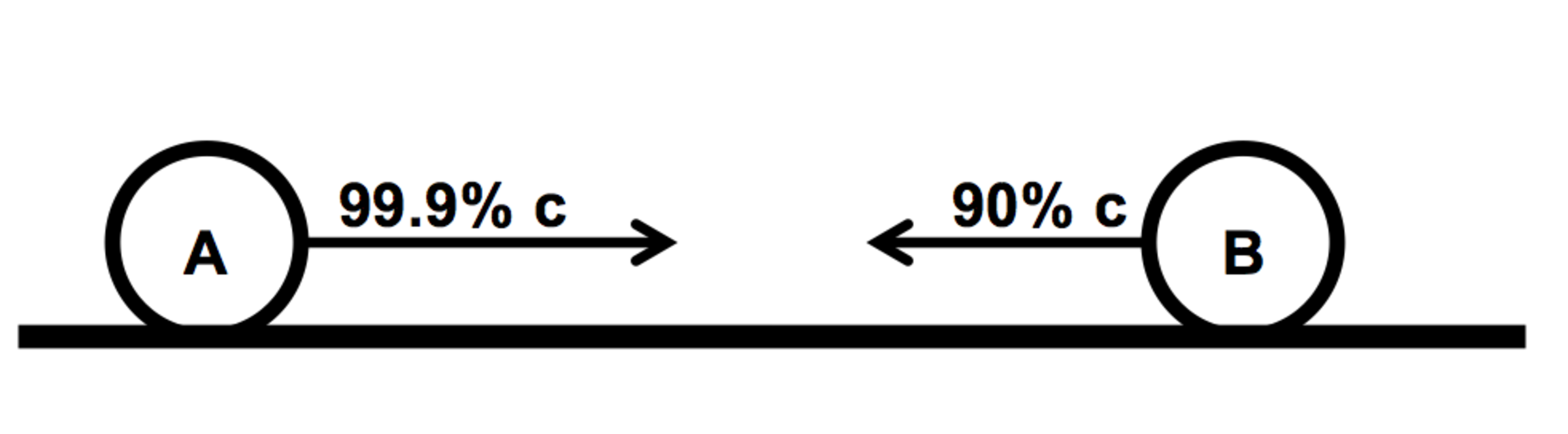
A particle (A) of rest mass 2 − 10 ^{-10} kg has a speed of 99.9% the speed of light. Another particle (B) of unknown mass has a speed of only 90% the speed of light. Particles A and B collide in a (linear) perfect elastic collision (the total kinetic energy is conserved). Furthermore, both particles retain the same speed as before the collision took place, but travel in the opposite direction.

Assuming all energy is conserved between the two particles what is the rest mass of Particle B in grams (to 2.d.p)?


The answer is 10.57.

Jack Purllant by Jack Purllant , 22, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Jack Purllant
Mar 31, 2016

First we must find the momentum of a, using the relativistic mass of Particle A:

Therefore p=6546066.144 k g m s − 1 kgms^{-1}

As this is a perfect elastic collision (p of A) = (p of B)

Therefore m of B = 10.568....x 1 0 − 3 10^{-3} kg = 10.57g

5 Helpful 0 Interesting 0 Brilliant 0 Confused

Your reasoning is correct but your calculation is incorrect. The correct answer is mass of B=10.568 grams. You made a mistake in your calculation of p. It seems you used 0.99 instead of 0.999 inside the square root in the denominator.

Art Magnus - 5 years, 2 months ago

Log in to reply

Thanks. I have updated the answer to 10.57.

In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" from the menu. This will notify the problem creator who can fix the issues.

Calvin Lin Staff - 5 years, 2 months ago

I am getting the same answer

viv goel - 5 years, 2 months ago

Log in to reply

I get at momentum of 1.34 kg m/s, and a much, much smaller mass.

Andrew Normand - 4 years, 4 months ago

Yep, I see what I've done now, very sorry about that, I've accidentally managed to miss out the extra nine on the v squared.

Jack Purllant - 5 years, 2 months ago

Log in to reply

For problems that you haven't worked on, there is an option that says "report problem".

For problems that you've answered completely (correct, all wrong, viewed solutions etc), the option will say "view reports", where you will be shown the report forum and you can file a report.

Calvin Lin Staff - 5 years, 2 months ago

You have certainly committed a calculation error

viv goel - 5 years, 2 months ago

Do note, you might want to convert the answer to grams from kilograms.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...