Impulses, impulses everywhere...

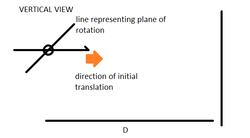Suppose a ball has been thrown at a wall at a speed 'u' from a height 'H' horizontally (parallel to the ground)

It is rotating at an angular velocity of $w\sqrt { 2 }$ in a plane making 45 degrees with the plane in which it was translating initially.

The wall is at a distance $D$ from the launch point,

such that

1) ${ 2u }^{ 2 }H<{ D }^{ 2 }g$

2) $D\quad <\quad u\sqrt { \frac { 2H }{ g } } +\frac { sin(2\quad arctan(\sqrt { \frac { gH }{ 2 } } ) }{ g }$

Let the friction on the floor be sufficiently high to just stop rotation ( See Note )

Find the average force it exerts on the wall when it collides with the wall provided the impact lasts for 2 seconds and it is perfectly elastic

if the answer is 'a'

input the square of a to the closest integer (if it is not an integer)

DETAILS AND ASSUMPTIONS

1) u (initial velocity)=0.7320 approximate as (root(3)-1)

2)w (initial angular velocity)=2.5

4)Mass of Ball=1

5)Radius of ball =1

All in S.I unit

NOTE

1) the inequalities are not the exact necessary conditions example,, if the question requires a<b then i may have altered it as a<b-1 because the second inequality naturally implies the first one,, so as to not reveal the answer,

2) also the figure shows a satelite view of the problem

3) Considering the balls rotation as a vector superposition of angular velocities along different axes might help

This problem was inspired by Let's play cricket