∆ in a O -- 1

Note that an inscribed triangle is acute if and only if it contains the center of the circle (either in its interior or on an edge). Otherwise, the largest angle would intercept an arc greater than $180^\circ$ . Given two points $A, B$ on a circle, the third point $C$ must lie in the red region below if $\triangle ABC$ is to be acute: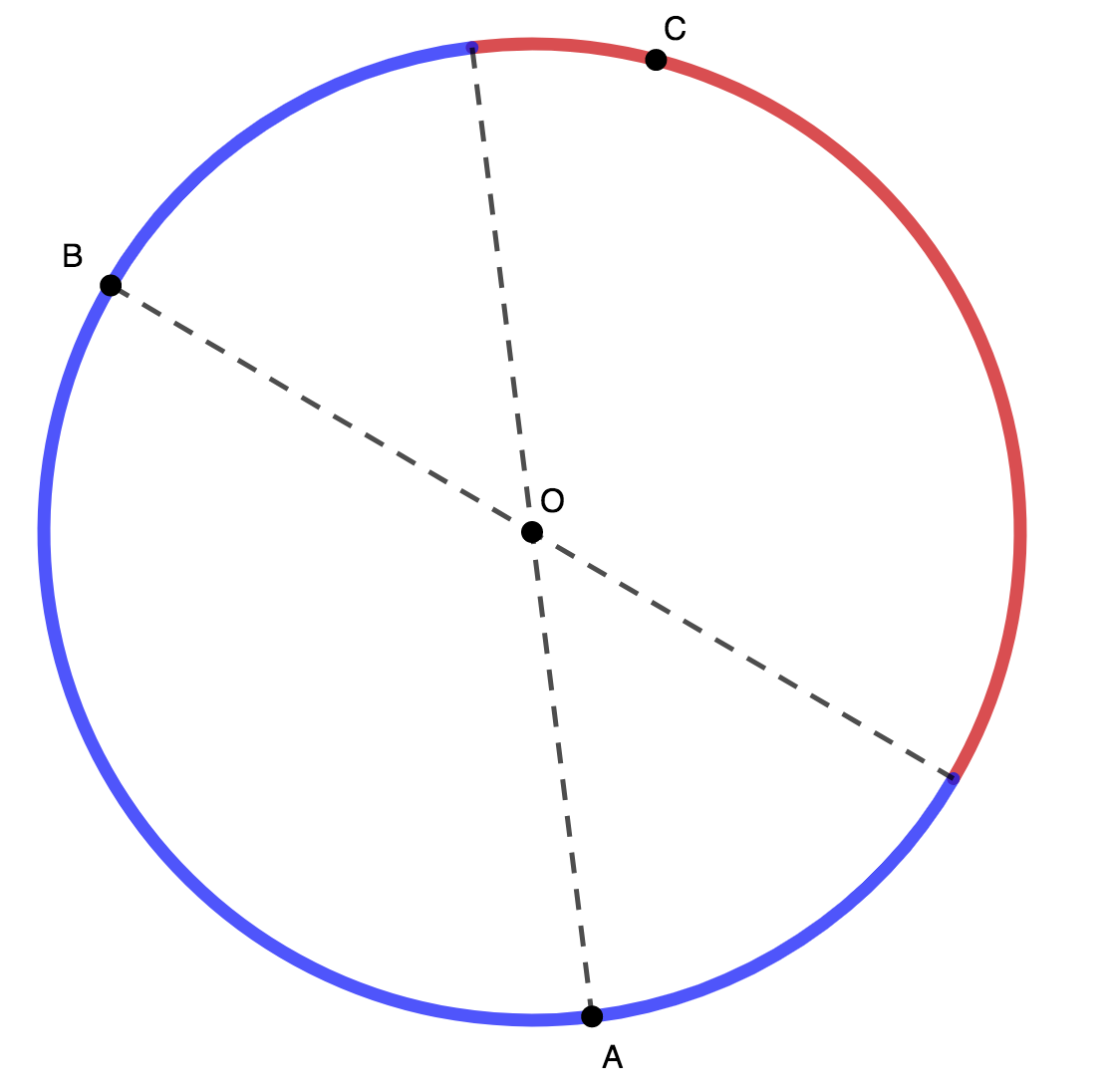

Now, we find the probability of this happening. Fix $A$ and $B$ on the circle, and let $\theta$ be the angle between them ( $\angle AOB$ ). Then $0<\theta\leq \pi$ . Note that the angle intercepting the red region in the diagram is precisely $\theta$ . Thus the probability of a random point $C$ being placed in the red area is $\frac{\theta}{2\pi}$ . We integrate to compute the average probability over all possible $\theta$ : $\frac{1}{\pi-0}\int_0^\pi \frac{\theta}{2\pi}\,\mathrm{d}\theta = \frac{1}{\pi}\left[\frac{\theta^2}{4\pi}\right]_{\theta=0}^\pi = \frac{\pi^2}{4\pi^2} = \frac{1}{4}=\boxed{0.25}$

An easier way to think about this problem is that this question is equivalent as 1- P(three point on the circle are within a semicircle). When the three points are within the semicircle, then the center will not be included in the triangle.

Let's now compute the probability part. Pick any point, say A, label the rest B,C. The probability that B and C are within the clockwise semicircle is 1/4. And we can pick A, B, and C as our starting point. Hence in total, the desired probability we would like to compute is 3/4. And the answer is 1-3/4 = 1/4.

An angle inscribed in a semi-circle is a right angle. So for an acute triangle, all three points must lie within a semi-circle. The probability is 1/8, but there are 2 semi-circles, so the answer is 1/4. Ed Gray