In Circles!
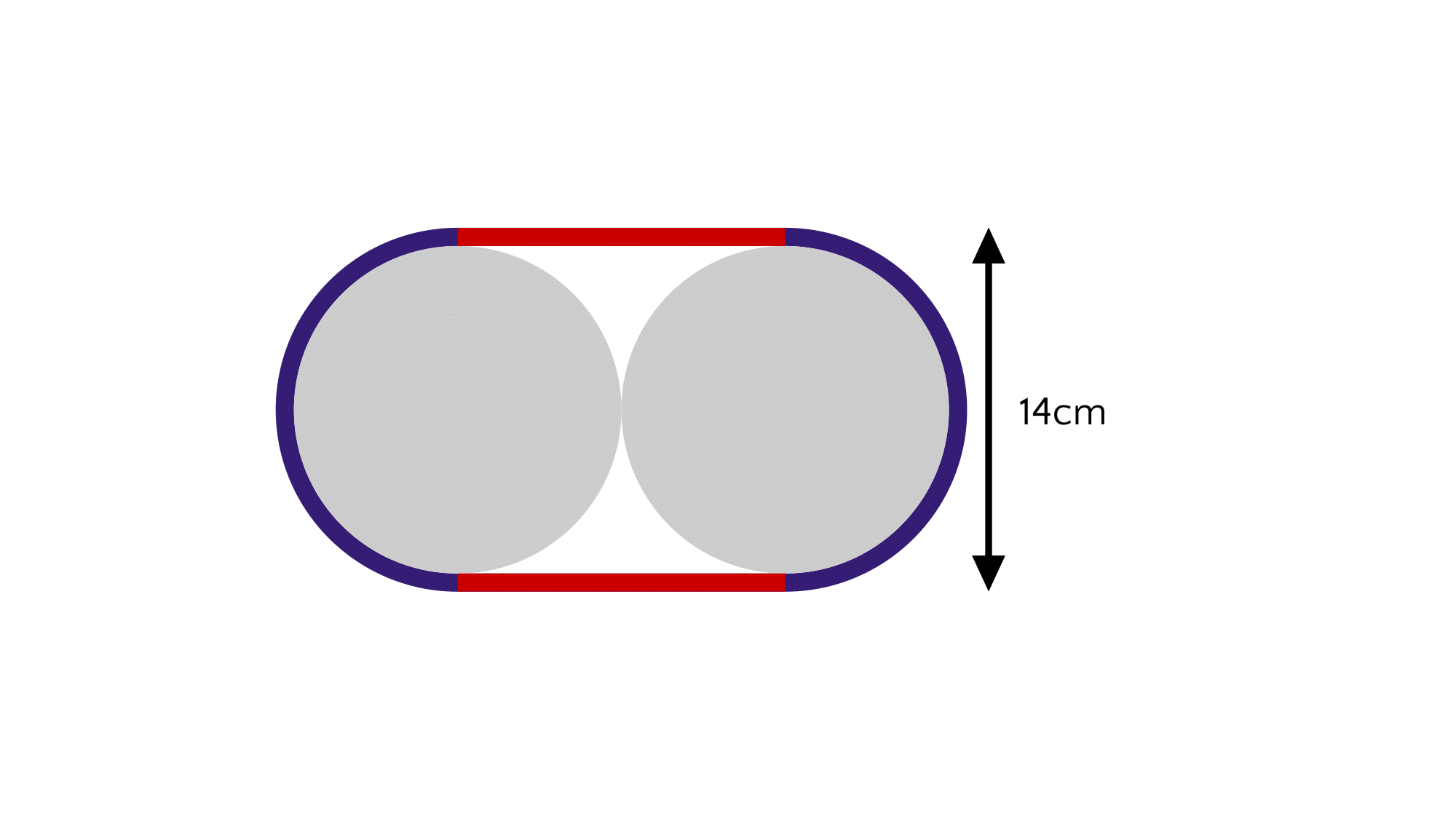
Two circles are put next to each other, of the same radius.
Then, a thick material is wrapped tightly around the circles, leaving no gaps; except for where the highest and lowest points of the circles, which make two parallel lines (highlighted in red).
If the vertical height of the whole shape is , what is the area of the whole shape (including the material around the circles and the gaps)? (in cm)
The answer is 321.938040026.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Sorry! Thanks to everyone who spotted my error(s). It should be fine now.
Here’s @Joshua Lawrence Garcia ’s solution to the problem, rewritten slightly.
We need to split this up into two factors and rejoin them together: in this scenario we’ll split up the material around the circles into the colours which they already have been.
We can split up the circles into semi-circles, and add on the blue parts for 2 semi-circles radius 7 c m . 2 semi-circles equals 1 circle, so that part of the area is 4 9 π c m .
The middle part turns out to be a rectangle - we know its height is 1 4 c m , but it turns out that by using radii of the original circles, we find out that its length is 1 2 c m . Therefore, the middle rectangle’s area must be 1 6 8 c m .
1 6 8 + 4 9 π = 3 2 2 c m (to 3s.f.)