In-e-qualities
Find the minimum value of a 2 + b 2 when 3 a + 4 b = 1 5 .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
not clear to me
Nice method :clappo:
By Cauchy’s Inequality :
|3a+4b|< a 2 + b 2 * 3 2 + 4 2 =5 a 2 + b 2
According to the given condition:
a 2 + b 2 > 5 1 5 = 3
Moderator note:
Right, it's easy to spot that Cauchy Schwarz Inequality is applicable because we have an expression where all the terms (inside the radical) are squared.
For the sake of variety, can you solve this geometrically? And via calculus, separately?
Calculus solution :
We only need to minimise a 2 + b 2 since x is a monotonically increasing function.
We first express b in terms of a : b = − 4 3 a + 4 1 5 . Then we get that a 2 + b 2 = a 2 + ( − 4 3 a + 4 1 5 ) 2 . To minimise this, we differentiate wrt a and set to 0 :
d a d [ a 2 + ( − 4 3 a + 4 1 5 ) 2 ] = 2 a + 2 ( − 4 3 a + 4 1 5 ) ( − 4 3 ) = 8 2 5 a − 8 4 5 = 0
(Here, we employed some assistance from the chain rule.)
Solving, we get a = 5 9 . Now, plugging it all back into the original expression, we have
a 2 + b 2 = a 2 + ( − 4 3 a + 4 1 5 ) 2 = ( 5 9 ) 2 + ( − 4 3 5 9 + 4 1 5 ) 2 = 9 = 3
Super nasty, though.
Geometric solution :
Notice the question is asking for the shortest distance between the origin and some point ( a , b ) on the linear graph 3 a + 4 b = 1 5 . Of course, that is when the distance between the origin and the line is perpendicular!

Here, I've marked out the distance in blue. How do we find it, then? We could do a tedious calculation, solving for a and b , of course; however, see that a triangle is formed, and we can use its area to get the distance.
Let our distance be x . Then
area of △ = 2 1 × 5 × 4 1 5 = 8 7 5 = 2 1 × 5 2 + ( 4 1 5 ) 2 x = 8 2 5 x
It's clear, then, that x = 3 .
Log in to reply
The easier way to think about this is that a 2 + b 2 = R is a circle. So we want to find the smallest circle which cuts this line, thus it would be tangential , and the radius would be perpendicular to the line. This is why we want the "perpendicular through the origin".
I thought that when adding squares that have bases that add to a constant, the smallest sum is when the bases are equal. So I set a=b and solved based on that. This did not get me the right answer, though it was close (within a couple hundredths). Can anyone explain why this is wrong?
Log in to reply
It is not always true that inequalities achieve their extrema when all terms are equal, even if they are symmetric / cyclic.
For example, see inequalities with strange equality conditions .
My way is trial and error, there's only 2 ways it could've worked. a=5 and b=0 or a=1 and b=3 and √25 is more than √10 so √10 is the obvious choice
Log in to reply
You seem to be assuming that a and b must be integers.
Is there any way we can solve this problem using the AM GM inequality?
There is a very nice solution to these kind of problems, we were taught in high school in Hungary, even in weaker ones. Look at this slick solution with vectors.
Look at the vectors (a,b) and (3,4). Take their scalar product.
One way to write it is $scalar=|a,b| |3,4| cos(gamma)=5cos(gamma)\sqrt{a^2+b^2}$
On the other hand, it equals: $scalar=x 1x 2+y 1y 2=3a+4b=15$ We get that $15=5cos(gamma)\sqrt{a^2+b^2}$ $3=cos(gamma)\sqrt{a^2+b^2}$. Since cos(gamma) is less or equal to 1, $\sqrt{a^2+b^2}$ is more or equal to 3.
Equality case: When gamma=0°.
Log in to reply
Indeed. That is the vector form of Cauchy Schwarz.
Another solution using trigonometry:
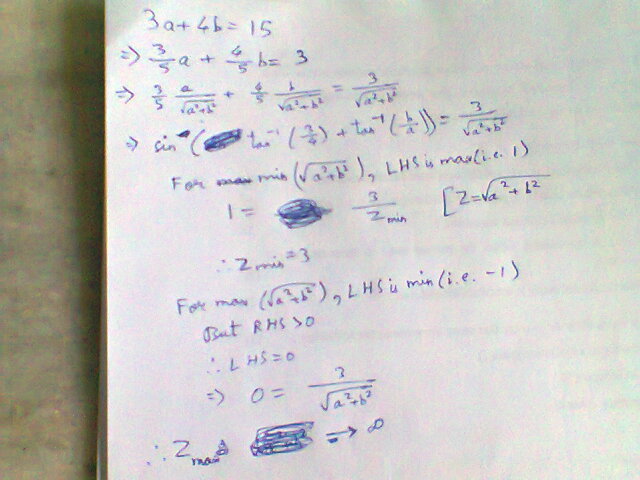
4b* not 6b
@Jackson Frey It's actually written '4', not '6'. My handwriting is on the poorer side, sorry :(
Can't it be done using AM-GM as follow 3a+4b >=√[(3a)(4b)] 15/2>=√(12ab) Min. Value of ab=225/48
Now a^2+b^2>=2ab Min. Value of a^2+b^2= 225÷24 Min.Value of √(a^2 + b^2) = √(225/4) =3.061 ~3
But can someone explain me why is small difference between two methods
Log in to reply
Applying AM-GM, you get maximum value of (a b), not minimum. Hence, the rest of the statements are not valid as if (a b)<(225/48), then sqrt(a^2 + b^2) may be less than 3.061, hereby resolving your doubt! :)
After calculating z(min)=3 you messed the answer although till there answer was correct.Very impressive and different from others!
Using straight lines ,consider the axes to be a and b ,instead of x and y. (a^2+b^2)^1/2 is nothing but distance from origin. Find the minimum distance from origin using formula for perpendicular distance ,which is abs.((Ax1+By1+c)/(A^2+B^2)^1/2 ) where A,B,C are the coefficients of the x and y respectively, in this case of a and b, and c is the constant term.(X1,y1) is the point from which distance is to be calculated , in this case (0,0). Applying this we get answer as 3
Yeah exactly! I did it by the same method... :)
Most elegant way!
From R . M . S . − A . M . :
x 2 + y 2 x 2 y 2 a 2 + b 2 = x 2 + y 2 y 2 ( x a ) 2 + x 2 ( y b ) 2 ≥ x 2 + y 2 y 2 ( x a ) + x 2 ( y b ) = x y x 2 + y 2 y a + x b
Letting y = 3 and x = 4 :
a 2 + b 2 ≥ 4 2 + 3 2 3 a + 4 b = 5 1 5 = 3
First we express a in terms of b, a= 3 1 5 − 4 b Then you need to express root a^2 + b^2 in terms of only b..(using the first equation) Then just differentiate it, find the minima, plug in the value
DONE
3 a + 4 b = 1 5 ⟹ b = 4 1 5 − 3 a . Hence, a 2 + b 2 = a 2 + ( 4 1 5 − 3 a ) 2 = 1 6 ( 5 a − 9 ) 2 + 1 2 2 ≥ 4 1 2 = 3 .