In my School......

take the number of students who wear spectacles as 'x'

.'. x - 60 students wear spectacles and don't bring lunch........ eq. 1

.'. {2(500 - x)}/3 students don't wear spectacles and don't bring lunch........... eq. 2

eq 1 is three times eq. 2 [eq. 1 equals 1/4 of students who don't bring lunch]

.'. 3x - 180 = {2(500 _ x)}/3

.'. 9x - 540 = 1000 - 2x

.'. 11x = 1540

.'. x = 140

substituting value of x in eq. 2 we get,

360 * 2/3 = 240

Let $NS$ be the set of students who do not wear spectacles and $NL$ be the set of students who do not bring lunch. The set of students who wear spectacles and who bring lunch is the complement of the set that is the union of sets $NS$ and $NL,$ and thus this union has $500 - 60 = 440$ students.

Letting $|A|$ represent the number of elements in any set $A,$ we then have that

$|NS \cup NL| = |NS| + |NL| - |NS \cap NL| = 440,$ (i).

We are given that $|NS \cap NL| = \dfrac{2}{3}|NS| = \dfrac{3}{4}|NL| \Longrightarrow |NL| = \dfrac{8}{9}|NS|.$

Plugging these results into equation (i), we find that

$|NS| + \dfrac{8}{9}|NS| - \dfrac{2}{3}|NS| = 440 \dfrac{11}{9}|NS| = 440 \Longrightarrow |NS| = 360.$

Thus the number of students who have neither spectacles nor a lunch is

$|NS \cap NL| = \dfrac{2}{3}|NS| = \dfrac{2}{3}*360 = \boxed{240}.$

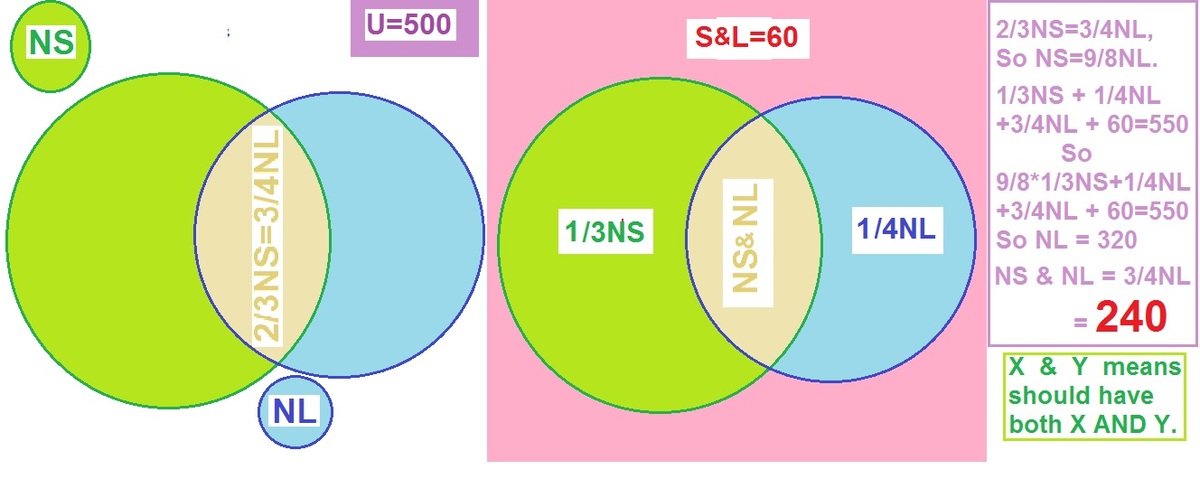
The sketch above gives one solution and solution below is another solution.
From simple logic. S students with spectacles , L taking lunch.
NS not S............. NL not L.
(1-2/3) NS+60=L=500-NL ...... $\implies$ NS + 3NL= 3 * 440.................(1)
(1-3/4)
NL+60=S=500-LS ...... $\implies$ NL + 4NS= 4 * 440.................(2)
(1)+(2)...................................................4NL +5NS= 7 * 440.................(3)
4(2)-(3).........................................................11NS =9* 440.
NS=360.......NL=320
Those not hot having at lest one = 360 +320 = 680.
But there are only 500 - 60 = 440 such students left.
$\implies\ 680 - 440 = \Large\ \ \ \color{#D61F06}{240}.$ are those not having spectacles nor lunch.