In the dark.
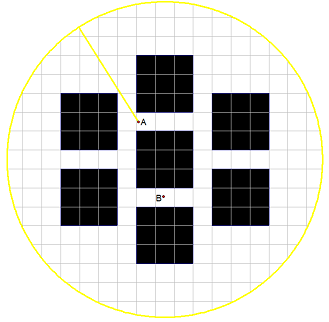
Seven squares are arranged on a unit grid as shown. From some positions within the squares, you can see to the outside as with point . On the other hand, point cannot see to the outside.
Find the area of the region(s) formed by all points that cannot see to the outside.
The answer can be written as an improper fraction which when fully reduced is Enter the value of
The answer is 74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
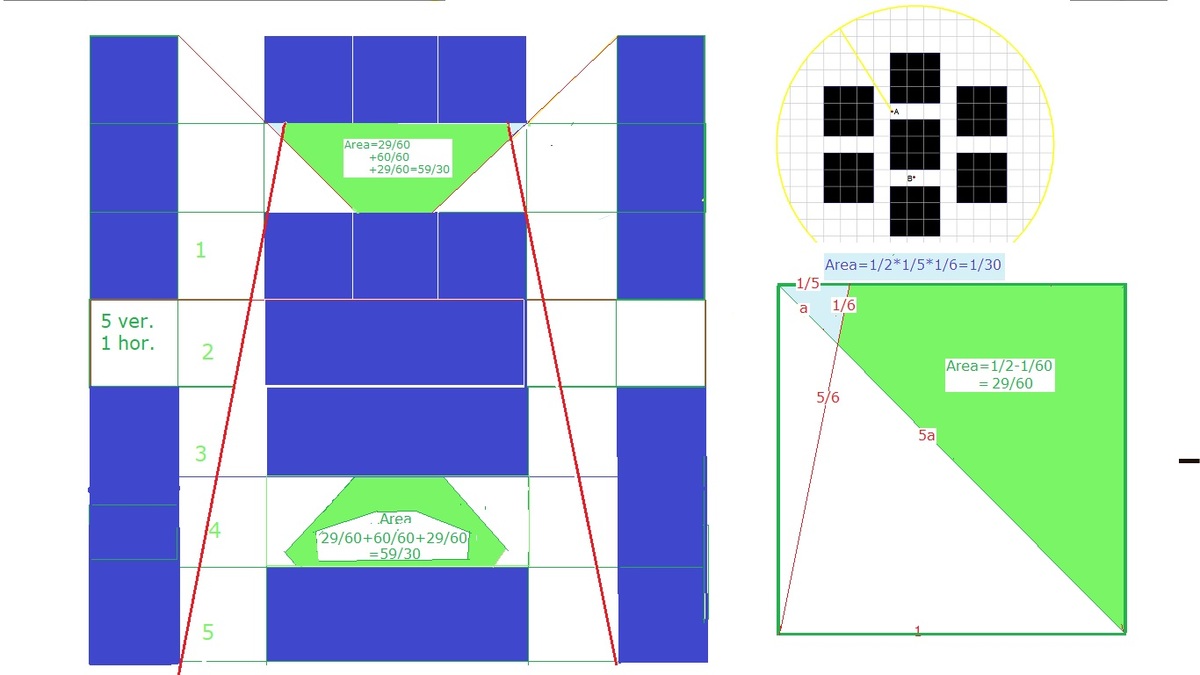
Here is a close-up view showing the regions in the dark in blue. We see two full squares and four triangles with a tiny corner trimmed off. So the area is 4 minus the 4 tiny corners.
Next is an even closer view of the upper left triangle. I added coordinates to help find the tiny corner, which is itself a triangle formed by the lines y = 1 − x , y = 1 , and y = 5 1 x . The area of this triangle is then A = 2 1 ⋅ 5 1 ⋅ 6 1 = 6 0 1 .
The four tiny corners then have area 4 ⋅ 6 0 1 = 1 5 1 .
The final area is 4 − 1 5 1 = 1 5 5 9 so the answer is 5 9 + 1 5 = 7 4