Incenter and ratios
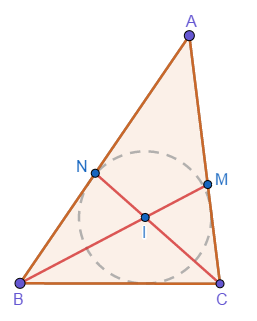
For △ A B C in the figure, we have the following information:
- B C = 4 .
- I is the incenter of △ A B C .
- M is the intersection point of lines B I and A C .
- N is the intersection point of lines C I and A B .
- B I : I M = 2 : 1 .
- C I : I N = 3 : 2 .
Find the area of △ A B C .
If it can be expressed as c a b , where a , b , and c are coprime positive integers and b is square-free, enter a + b + c as your answer.
Note: M and N are not necessarily tangential points of the incenter and the triangle.
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
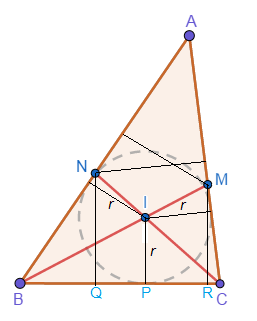
Let the inradius be r and side lengths B C = u = 4 , A C = v , and A B = w . Then the area of △ A B C , [ A B C ] = 2 1 ( u + v + w ) .
As △ C I P and △ C N Q are similar, we have I P N Q = C I C N = 3 5 , ⟹ N Q = 3 5 r . Then area of △ B C N , [ B C N ] = 6 5 r u . Similarly, [ A C N ] = 6 5 r v . Note that [ A B C ] = [ B C N ] + [ A C N ] = 6 5 r ( u + v ) .
Similarly, △ B I P and △ B M R are similar, we have I P M R = B I B M = 2 3 , ⟹ M R = 2 3 r . Then area of △ B C M , [ B C M ] = 4 3 r u . Similarly, [ A B M ] = 4 3 r w . Note that [ A B C ] = [ B C M ] + [ A B M ] = 4 3 r ( u + w ) .
Then, we have [ A B C ] = 6 5 r ( u + v ) = 4 3 r ( u + w ) = 2 1 r ( u + v + w ) . Therefore,
6 5 ( u + v ) 5 ( u + v ) ⟹ w = 2 1 ( u + v + w ) = 3 ( u + v + w ) = 3 2 ( u + v ) . . . ( 1 )
4 3 ( u + w ) 3 ( u + 3 2 ( u + v ) ) ⟹ v ⟹ w = 2 1 ( u + v + w ) . . . ( 2 ) = 2 ( u + v + 3 2 ( u + v ) ) = 4 5 u = 5 = 3 2 ( u + v ) = 6 Since w = 3 2 ( u + v )
By Heron's formula ,
[ A B C ] = s ( s − u ) ( s − v ) ( s − w ) = 2 1 5 ⋅ 2 7 ⋅ 2 5 ⋅ 2 3 = 4 1 5 7 where s = 2 u + v + w = 2 1 5
Therefore, a + b + c = 1 5 + 7 + 4 = 2 6 .
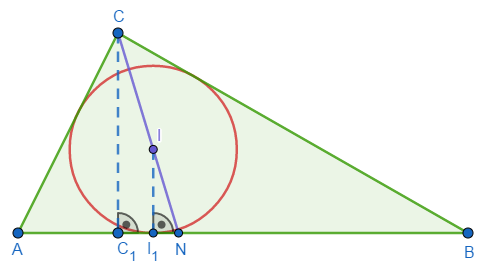
Let C 1 and I 1 be orthogonal projections of C and I , respectively, on side A B . Then C C 1 = h c is the altitude of △ A B C adjacent to side A B and I I 1 = r is the radius of the incircle. Both of these lines are perpendicular to A B so C C 1 ∣ ∣ I I 1 and △ C C 1 N ∼ △ I I 1 N . By similarity:
r h c = I I 1 C C 1 = I N C N = I N C I + I N = 1 + I N C I
We can find another relationship between h c and r using formulas for area of △ A B C :
2 A B × h c = 2 A B + B C + C A r r h c = A B A B + B C + C A 1 + I N C I = 1 + A B B C + C A I N C I = A B B C + C A
Similarly, considering altitude from B and point M as in the figure in problem statement, we get:
I M B I = C A A B + B C
So far, we have: A B B C + C A = I N C I = 2 3 C A A B + B C = I M B I = 2
Since we know that B C = 4 , solving this system of equations gives us: A B = 6 and C A = 5
Now we can find the area using Heron's formula: S ( S − A B ) ( S − B C ) ( S − C A ) = 4 1 5 7 , where S = 2 A B + B C + C A = 2 1 5 is the semiperimeter of △ A B C .
The answer is 1 5 + 7 + 4 = 2 6 .


Since the incenter is the intersection of all the triangle's bisectors, then by the angle bisector theorem , I M B I = C M B C = A M A B and I N C I = B N B C = A N A C .
From I M B I = C M B C we have 2 = I M 4 or I M = 2 , and from I N C I = B N B C we have 2 3 = B N 4 or B N = 3 8 .
From I M B I = A M A B we have 2 = A C − 2 A B , and from I N C I = A N A C we have 2 3 = A B − 3 8 A C , and these two equations solve to A B = 6 and A C = 5 .
Thus △ A B C has sides 4 , 5 , and 6 , and by Heron's Formula its area is A = 4 1 5 7 , so a = 1 5 , b = 7 , and c = 4 , and 1 5 + 7 + 4 = 2 6 .