Incentroid

Let the lengths of the legs be $a$ and $b$ as shown. The angle bisectors are the blue segments and meet at the incenter. The medians are the red segments and meet at the centroid. The projections of these points onto the legs are shown and distances are given in terms of $a$ and $b$ .

$a/3 - b/3 =1$ so $a=b+3$

$\tan \frac{\theta}{2}= \frac{b/3}{2b/3}=\frac{1}{2}$ from which $\tan \theta = \frac{4}{3} = \frac{a}{b}$

Substituting gives $\frac{b+3}{b}=\frac{4}{3}$

From which $b=9$ , $a=12$ and by Pythagoras $c=15$ . So the perimeter is $a+b+c=12+9+15=\boxed{36}$

Realizing that the length of the segment could be scaled by scaling the triangle, I assumed a height of the triangle with its right angle at the origin of 1 and a base of $x$ . The triangle's centroid would be at $\left\{\frac{x}{3},\frac{1}{3}\right\}$ under those conditions. Using a description of the incenter computation , I derived a formula for the height of the centroid under those conditions and solved it for being equal to $\frac13$ : $\frac{x}{\sqrt{x^2+1}+x+1}=\frac{1}{3} \Longrightarrow x\to \frac{4}{3}$ . Using $x=\frac43$ in formula for the centroid gave location of the centroid as $\left\{\frac{4}{9},\frac{1}{3}\right\}$ . Noting that the $y$ height is $\frac13$ as desired, I continued. The Euclidean distance between the incenter and the centroid is $\frac49-\frac13\Longrightarrow\frac19$ . Now the scaling factor is known to be $9$ . The perimeter of the original triangle, the sum of the three sides $\left\{\frac{5}{3},1,\frac{4}{3}\right\}$ is $4$ . Therefore, the answer is $4\times 9\longrightarrow 36$ .

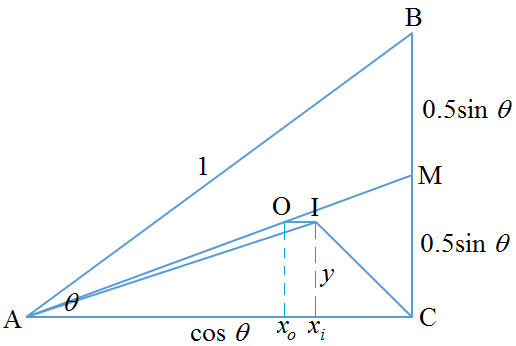
Let the right triangle be $ABC$ , where $\angle C = 90^\circ$ , $\angle A = \theta$ , and $AB = 1$ . Then $BC = \sin \theta$ and $AC=\cos \theta$ . Let $M$ be the midpoint of $BC$ , $I$ , the incenter, $O$ , the centroid, $A$ be the origin of $xy$ -plane and $OI$ be parallel to $AC$ .

Then the $y$ coordinate of $I$ is given by

$\begin{aligned} \tan \angle IAC & = \frac y{\color{#3D99F6}x_i} & \small \color{#3D99F6} \text{where }x_i \text{ is the }x \text{ coordinate of }I. \\ \tan \frac \theta 2 & = \frac y{\cos \theta - y} \\ \implies y & = \frac {\tan \frac \theta 2 \cos \theta}{1+\tan \frac \theta 2} & ...(1) \end{aligned}$

The $y$ coordinate of $O$ is given by $y = \dfrac 12 \sin \theta \times \dfrac 23 = \dfrac 13 \sin \theta \quad ...(2)$ .

From $(2)=(1)$ :

$\begin{aligned} \frac 13 \sin \theta & = \frac {\tan \frac \theta 2 \cos \theta}{1+\tan \frac \theta 2} \\ \frac 13 \tan \theta & = \frac {\tan \frac \theta 2}{1+\tan \frac \theta 2} & \small \color{#3D99F6} \text{Let }t = \tan \frac \theta 2 \\ \frac 13 \times \frac {2t}{1-t^2} & = \frac t{1+t} \\ \frac 2{3(1-t)} & = 1 \\ \implies t & = \tan \frac \theta 2 = \frac 13 \end{aligned}$

Therefore, $\tan \theta = \dfrac {2t}{1-t^2} = \dfrac {\frac 23}{1-\frac 19} = \dfrac 34$ $\implies \sin \theta = \dfrac 35$ and $\cos \theta = \dfrac 45$ . And

$\begin{aligned} y & = \frac {t \cos \theta}{1+t} = \frac {\frac 13 \times \frac 45}{1+\frac 13} = \frac 15 \\ x_i & = \cos \theta - y = \frac 45 - \frac 15 = \frac 35 \\ x_o & = \frac 23 \cos \theta = \frac 23 \times \frac 45 = \frac 8{15} \end{aligned}$

Therefore $OI = x_i - x_o = \dfrac 1{15}$ . To make $OI' = 1$ , we multiply all linear dimensions by 15. Hence $AB' = 1 \times 15 = 15$ , $BC' = 15\sin \theta = 9$ , $AC'=15\cos \theta = 12$ , and the perimeter of $\triangle ABC'$ is $\boxed{36}$ .

It is worth noting that any triangle $ABC$ with sides $a = c+3$ , $b = c+6$ and $c > 3$ is a triangle such that $IG$ is parallel to $BC$ and $IG = 1$ , where $I$ is the incentre and $G$ the centroid. The case $c=9$ gives the right-angled triangle case asked for by the question, with $B = 90^\circ$ , giving a perimeter of $\boxed{36}$ .

To prove this, suppose that $ABC$ is a triangle with $IG$ parallel to $BC$ and $IG = 1$ Also suppose that $b \ge c$ . Also suppose that $A \neq 90^\circ$ . Then $BC$ is not a diameter of the circumcircle of $ABC$ . If we choose our origin $O$ to be the circumcentre of the triangle $ABC$ , so that $\overrightarrow{OA}$ . $\overrightarrow{OB}$ . $\overrightarrow{OC}$ all have the same length, then $\overrightarrow{OB} + \overrightarrow{OC}$ is a nonzero vector perpendicular to $\overrightarrow{BC}$ , and so we require that $\overrightarrow{IG} \cdot \big(\overrightarrow{OB} + \overrightarrow{OC}\big) \; = \; 0$ Since $\overrightarrow{OI} \; = \; \frac{1}{a+b+c}\big[a\overrightarrow{OA} + b\overrightarrow{OB} + c\overrightarrow{OC} \big] \hspace{2cm} \overrightarrow{OG} \; = \; \tfrac13\big[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\big]$ the fact that $IG$ is parallel to $BC$ tells us (after much simplification) that $4\sin B \sin C \cos A(2a - b - c) \; = \; 0$ and hence $2a = b+c$ . But then $\overrightarrow{IG} \; = \; \frac{b-c}{3(b+c)}\overrightarrow{BC}$ and so we deduce that $(b-c)a = 3(b+c)$ . This leads us to $a = c+3$ and $b = c+6$ . We must have $c > 3$ for $ABC$ to be nondegenerate.

It is also possible to show that we cannot have a nondegenerate triangle $ABC$ with $IG$ parallel to $BC$ and $A = 90^\circ$ Using the notation of Ajit's solution, $\overrightarrow{IG} \cdot \binom{b}{a} \; = \; \tfrac16\big(a+b - \sqrt{a^2+b^2}\big)\big(2\sqrt{a^2+b^2} - a - b\big) \; \neq \; 0$ which shows that such a triangle is impossible.

Consider the right triangle formed by (0,0), (a,0) & (0,b). The in-centre,I will be at (r,r) where r=(a+b-√(a²+b²))/2 and the centroid G will be at (a/3,b/3). However, since IG is parallel to one of the legs with a unit length we may say that a/3 =(r+1) and b/3 =r assuming a>b and thus r={3(r+1)+3r-√((3(r+1))²+(3r)²)}/2 which yields r=3, the only admissible root. So a=12 & b=9 while the perimeter, p=9+12+15=36.