Incircle Riddle
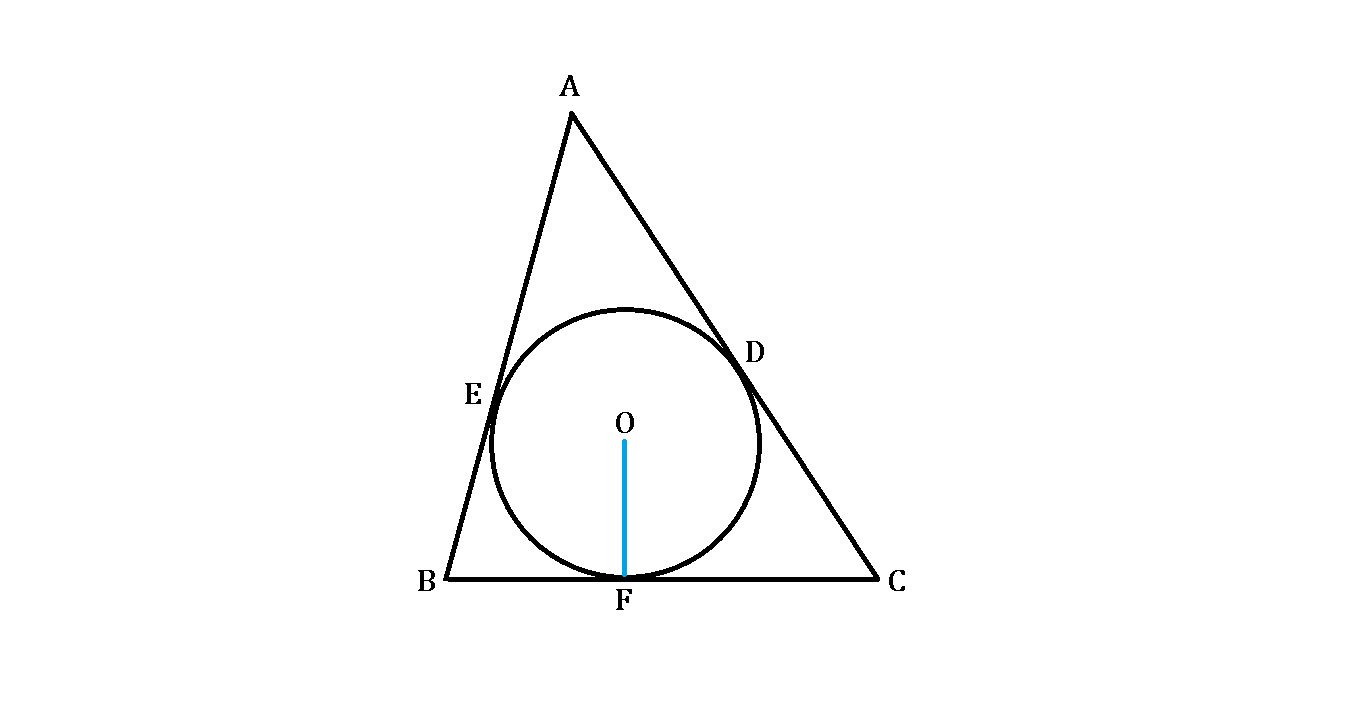
A triangle A B C has an incircle O , and D , E , F are the touching points on the triangle tangents, as shown above.
The 3 side lengths of A B C are pairwise coprime integers, where points D , E , F each divide those sides into 2 smaller integer lengths as well. Moreover, the triangle's perimeter can be written as both the sum and the difference of 2 perfect squares.
If the incircle's radius is 3, what is the least possible area of the triangle A B C ?
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I had posted an alternating solution . But it is edited out !!!!!
So I am posting it here.
Let us see if ABC is a right triangle at B, with inradius r = 3.
At B, the two tangents and corresponding radii at points of tangency
form a 3x3 square.
So the side have to be >3.
Let us see a few pythagorean triples, r=3 and sides >3.
r
=
1
/
2
(
a
+
b
+
c
)
1
/
2
a
b
=
a
+
b
+
c
a
b
.
(
5
,
1
2
,
1
3
)
.
.
.
.
.
.
r
=
5
+
1
2
+
1
3
5
∗
1
2
=
2
.
(
7
,
2
4
,
2
5
)
.
.
.
.
.
.
r
=
7
+
2
4
+
2
5
7
∗
2
4
=
3
.
.
.
.
.
.
.
.
B
u
t
7
+
2
4
+
2
5
=
5
6
i
s
n
o
t
a
s
u
m
a
n
d
a
d
i
f
f
e
r
e
n
c
e
o
f
t
w
o
s
q
u
a
r
e
s
.
(
8
,
1
5
,
1
7
)
.
.
.
.
.
.
r
=
8
+
1
5
+
1
7
4
∗
1
5
=
3
.
.
.
.
.
.
.
.
.
8
+
1
5
+
1
7
=
4
0
=
6
2
+
2
2
=
1
1
2
−
9
2
.
A
r
e
a
Δ
A
B
C
=
2
1
∗
8
∗
1
5
=
6
0
.
The angles angle bisectors make with the sides are A/2, B/2, C/2.
Also A/2+B/2+C/2=90.
So CotA/2=3/k, CotB/2=3/m, CotC/2=3/n, where k, m, n are tangent lengths from respective vertices.
But CotP+CotQ+CotR=CotP * CotQ * CotR when P+Q+R=90.
So 3/k+3/m+3/n=3/k * 3/m * 3/n.
⟹ 9 = k + m + n k ∗ m ∗ n .
Solving (k,m,n)=(3, 5,12).
So the sides are (8, 15, 17), a pythagorean triple.
So area =1/2 * 8 * 15= 6 0 .
8+15+17=40=6 * 6 + 2 * 2=11 * 11 - 9 * 9.