Inclined plane
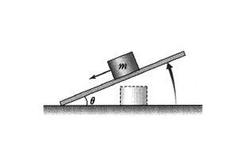 In the above figure, the angle
between the inclined plane and the floor is being increased gradually, until the object with mass
m
starts to slide down the slope at
Find the
coefficient of static friction
between the plane and the object.
In the above figure, the angle
between the inclined plane and the floor is being increased gradually, until the object with mass
m
starts to slide down the slope at
Find the
coefficient of static friction
between the plane and the object.
Gravitational acceleration is m/s
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
there's a formula for the coefficient of friction .....tan(theta)=coeff of friction ......where theta is the angle of the slope ........using that .....tan(45)=1=coeff of friction