Inclined string on an incline plane
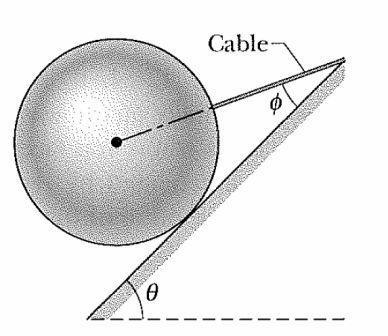 In the figure above, a 10 kg sphere is
supported on a frictionless plane inclined
at angle
θ
= 45° from the
horizontal. The angle
ϕ
is 25°. Calculate
the tension in the cable (in N).
In the figure above, a 10 kg sphere is
supported on a frictionless plane inclined
at angle
θ
= 45° from the
horizontal. The angle
ϕ
is 25°. Calculate
the tension in the cable (in N).
Liked it? try some more
The answer is 76.4602.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I was trying with g=10 SI units. You must mention g properly.
Yes indeed it is !
Log in to reply
Could you please tell me how to add diagrams in solutions? :D
Log in to reply
Yes, you can use markdown links. Go to an image sharing site (say imgur.com), and upload your image there; then type  , and you're done!
Hey but what if we resolve the forces perpendicular to the plane ???? Then we don't get the same result??
i took g=10.you had to mentioned that😞
Good solution. Up voted.
Wtf you didnt say g = 9.8
By a free boddy diagram
∑ x = m g sin 4 5 ° − T c o s 2 5 ° = 0
m g sin 4 5 ° = T cos 2 5 °
T = cos 2 5 m g sin 4 5 °
T = cos 2 5 ° 9 8 × sin 4 5 ° ≈ 7 6 . 4 6
I did by resolving forces along vertical and horizontal. But resolving along the inclined is definitely the best solution.
Abhishek, is this a problem of book Resnic Halliday (Principles of Physics).?
If we resolve mg parallel to the plane.It will come out to be
m g s i n θ (in downward direction)
and if we resolve Tension in the string(T) parallel to the plane. It will come out to be
T c o s ϕ (in upward direction)
As sphere is at rest so
m g s i n θ = T c o s ϕ
So
T = c o s ( 2 5 ) 2 9 8
On putting value of cos(25) we will get T=76.46N
It will be nice to explain with diagram.Could anyone tell me how to add diagrams in solutions?