Inclined Terminal.
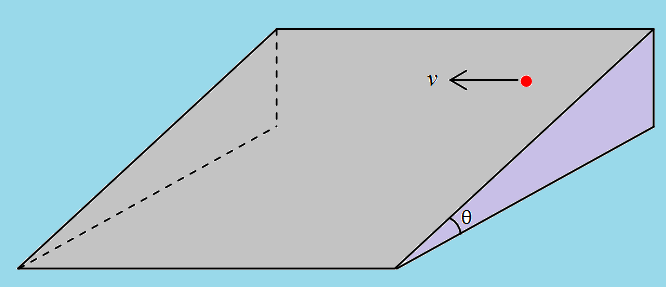 A particle is placed on a fixed rough inclined plane which makes an angle
from ground. The co-efficient of friction between between the particle and the inclined plane is
.
A particle is placed on a fixed rough inclined plane which makes an angle
from ground. The co-efficient of friction between between the particle and the inclined plane is
.
The particle is given a velocity along the line which is common to the inclined plane and the horizontal plane at that height.
Find the magnitude of terminal velocity (in ) attained by the particle.
Given Data : . Assume that the inclined plane is very large so that the particle never leave that plane.
Try more from my set Classical Mechanics Problems .
The answer is 4.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let first define the Cartesian Axes as follow: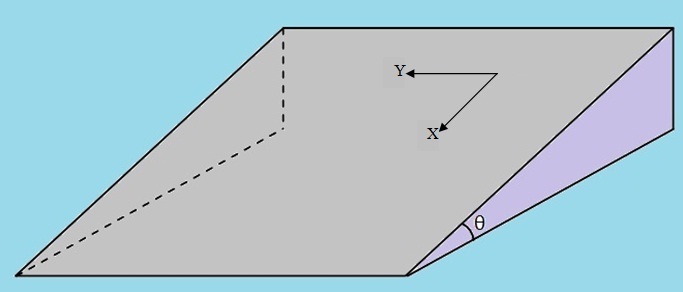
Also let the velocity of the particle be u at any instant and makes an angle α with X-axis as shown.
Also let the velocity of particle be u x & u y along X-axis & Y-axis respectively at that instant.
Now draw the free body diagram of the particle. It will be like as below. (I have not mention the normal reaction on the particle. It will be perpendicular and outward to our defined axes).
Now along X-axis we can write
m g s i n θ − f c o s α = m d t d u x
And along Y-axis we can write
f s i n α = − m d t d u y
Dividing both equations we get.
f s i n α m g s i n θ − f c o s α = − d u y d u x
⟹ c o s e c α − c o t α = − d u y d u x
⟹ u y u x 2 + u y 2 − u x = − d u y d u x
⟹ u x 2 + u y 2 d u y = u x d u y − u y d u x
The solution of this differential equation is ( u y ) 2 = c 2 − 2 c u x where c is a constant.
When u x = 0 then u y = v . This gives c = v .
Now when u y = 0 then 0 = v 2 − 2 v u x
So u x = 2 v = 4 . 5 m s − 1