Incoming!
A spacecraft approaching Earth very quickly is observed at a distance of D . This has never happened before, so you check your instruments for time Δ t , and then you check the position of the craft again.
Now you can see it at a distance of D − 3 c Δ t , where c is the speed of light.
The craft is traveling at a constant speed of v directly toward Earth. What is v ?
Assume you have made your measurements from an inertial frame very close to Earth.
Hint: The correct solution requires no transformation.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Although I answered correctly, I think that this is not the correct answer to the problem like it's written or that problem is not well posed. It says: "Spacecraft is observed at a distance of D . This has never happened before, so you check your instruments for time Δ t and then you check the position of the craft again" . I understood it that you check the instruments for time Δ t and then send another signal which will now meet the spacecraft at the distance D − 3 c Δ t , for which it will take time t ′ ′ = c D − 3 c Δ t , that will provide spacecraft to get closer to Earth by extra υ × c D − 3 c Δ t . Here's the picture:
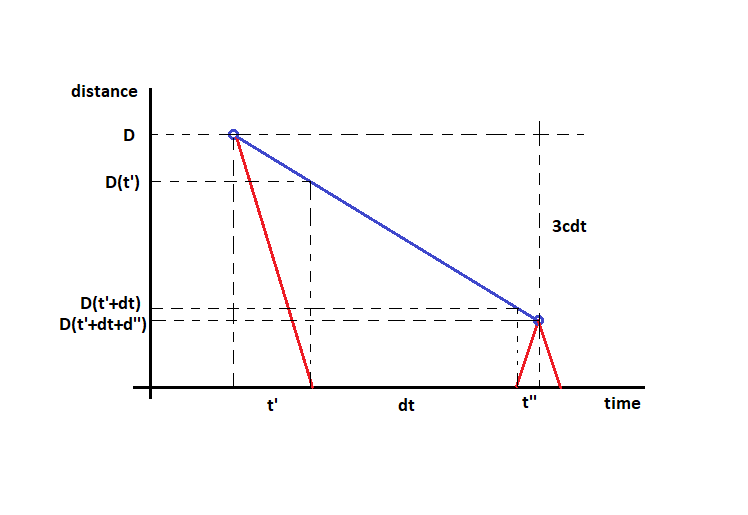
Log in to reply
It's not that you send a signal which then returns, the ship is always sending out signals to you. So the second signal you receive is not after you've sent it and had to wait for it to bounce back, it's just a signal from the second ship. Additionally, the question does not mention any method of sending a signal, I assumed that the signal we were using was something along the lines of visible light through a telescope, as it simply says "observed."
Also, the diagram in the question is pretty much exactly the same as my diagram, except turned sideways.
Log in to reply
I see now, thank you! I didn't actually pay much attention to the diagram and, as you said, it clears out things.
This reminds me why I am not a mathematician, or a physicist.
I think for this perhaps the assumption is that some EM signal from the sun or other source is being reflected, rather than observer is signalling.
If the problem had stated that the ship was AT point D initially and then AT point D - (3c del t) after passage of time del t (rather than observed from earth at those times to be at those positions), would v = 3c? Since del Position = -3c del t, and del P/del t = -3c and that should be velocity.
Although something coming at you faster than the speed of light can't be seen or observed by EM, I think ... just like you can't hear the bullet that hits you (strike precedes the sound waves). So the Klingons approaching at warp can't be seen?
Just some tangential thoughts.
Pretty much good.
My solution is based on the fact that while the light from the observations is moving towards the earth the spaceship is also getting closer. Let D 1 and D 2 be the first and second observed distances. The times taken for the light to reach the earth from these observations are c D 1 and c D 2 respectively
Then, if the speed of the spaceship is v , the actual distances of the spaceship at the moment the observations are made are
D 1 − c D 1 v and D 2 − c D 2 v
Take the difference of these to see that the actual distance travelled by the space ship between the observations is
( 1 − c v ) ( D 1 − D 2 )
We are told in the question that D 1 − D 2 = 3 c Δ T substituting this into the above expression and dividing by Δ T to find the velocity gives an easy equation -
v = ( 1 − c v ) 3 c
leading to the solution v = 4 3 c
Does this solution require an instantaneous measurement? Surely the measurement itself, which is not stated in the problem, needs to take some time?
Log in to reply
There is an unstated assumption that the time taken to take the measurement, is much less than Δ T , and that any errors in the measurement are much less than the reported distances.
It is not usual to worry about these things in a problem of this type unless the errors are an explicit part of the question. But in real life - if an alien space ship were detected approaching earth - every assumption would be critically examined!
By taking the initial time (
t
0
) as the time when when we first observe the spaceship, then the second time we observe the spaceship it is
t
0
+
Δ
t
.
Therefore it has been
c
D
time for the light to reach the observer at
t
0
.
Then, in the time
Δ
t
the spaceship travels for time
v
3
c
Δ
t
, since it’s distance travelled is
3
c
Δ
t
because:
D
−
(
D
−
3
c
Δ
t
)
=
3
c
Δ
t
After which its light then travels for time
c
D
−
3
c
Δ
t
.
Overall the time prior to
t
0
at which the spaceship is at distance
D
is:
c
D
and the time prior to
t
0
+
Δ
t
at which the spaceship is at distance
D
−
3
c
Δ
t
is:
c
D
−
3
c
Δ
t
+
v
3
c
Δ
t
Therefore prior to
t
0
at which the spaceship is distance
D
−
3
c
Δ
t
is:
c
D
−
3
c
Δ
t
+
v
3
c
Δ
t
−
Δ
t
At which point the two values of time ellapsed prior to
t
0
are equal and can be equated and rearranged for
v
. This gives:
c
D
=
c
D
−
3
c
Δ
t
+
v
3
c
Δ
t
−
Δ
t
Multiplying by
c
and
v
gets rid of fractions:
D
v
=
D
v
−
3
c
v
Δ
t
+
3
c
2
Δ
t
−
c
v
Δ
t
Simplifying gives:
4
c
v
Δ
t
=
3
c
2
Δ
t
Cancelling out
Δ
t
and
c
results in:
v
=
4
3
c
.
Assume that the second signal received was emitted at at time Δ τ after the first signal was emitted. Δ τ > Δ t because the second signal took less time to get to the earth.
The time between the reception of the signals is Δ t = Δ τ + c − Δ D = ( − Δ D ) ( − v 1 + c 1 ) , where we used Δ D = − v Δ τ . Thus Δ D = − v 1 − c 1 1 Δ t = − c − v v c Δ t . Since we are told that the right-hand side equals − 3 c Δ t , we conclude c − v v = 3 ∴ v = 4 3 c .
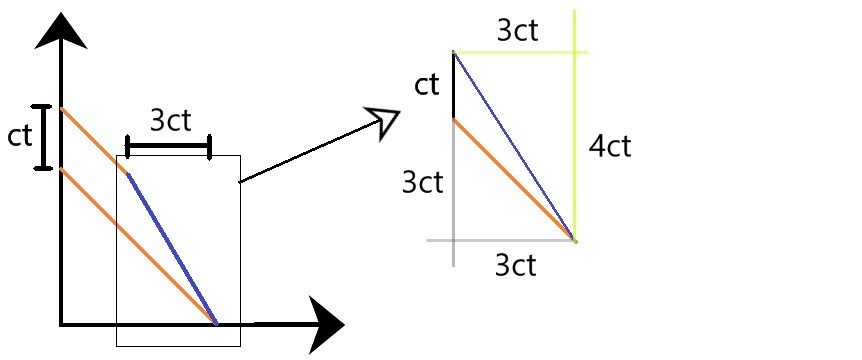
Compare the weak green lines, get c v = 4 3 .
Here is a distance vs time graph of the scenario. The path of the ship is shown in blue, moving from A to E, while the path of the light rays moving from the ship to the Earth are shown in red.
Notice how the path of the light rays have a constant slope. This slope is the speed of light, c .
This is all the working out shown in the image:
The observed difference in time between the light rays is Δ t , so the line FE is also Δ t , as is BC. Note that this is not the same as AC, the time in which the ship has moved between the two observed distances.
The ship moves a distance of 3 c Δ t between the two points, as given in the question, which is the length of CE.
If the ship is moving at a constant speed v , then we can find AC in terms of v : t i m e = s p e e d d i s t a n c e A C = v 3 c Δ t .
Now we can form an equation with the lengths of the top lines: A C = A B + B C v 3 c = 3 Δ t + Δ t v 3 c = 3 + 1 v = 4 3 c