Inconvenient points
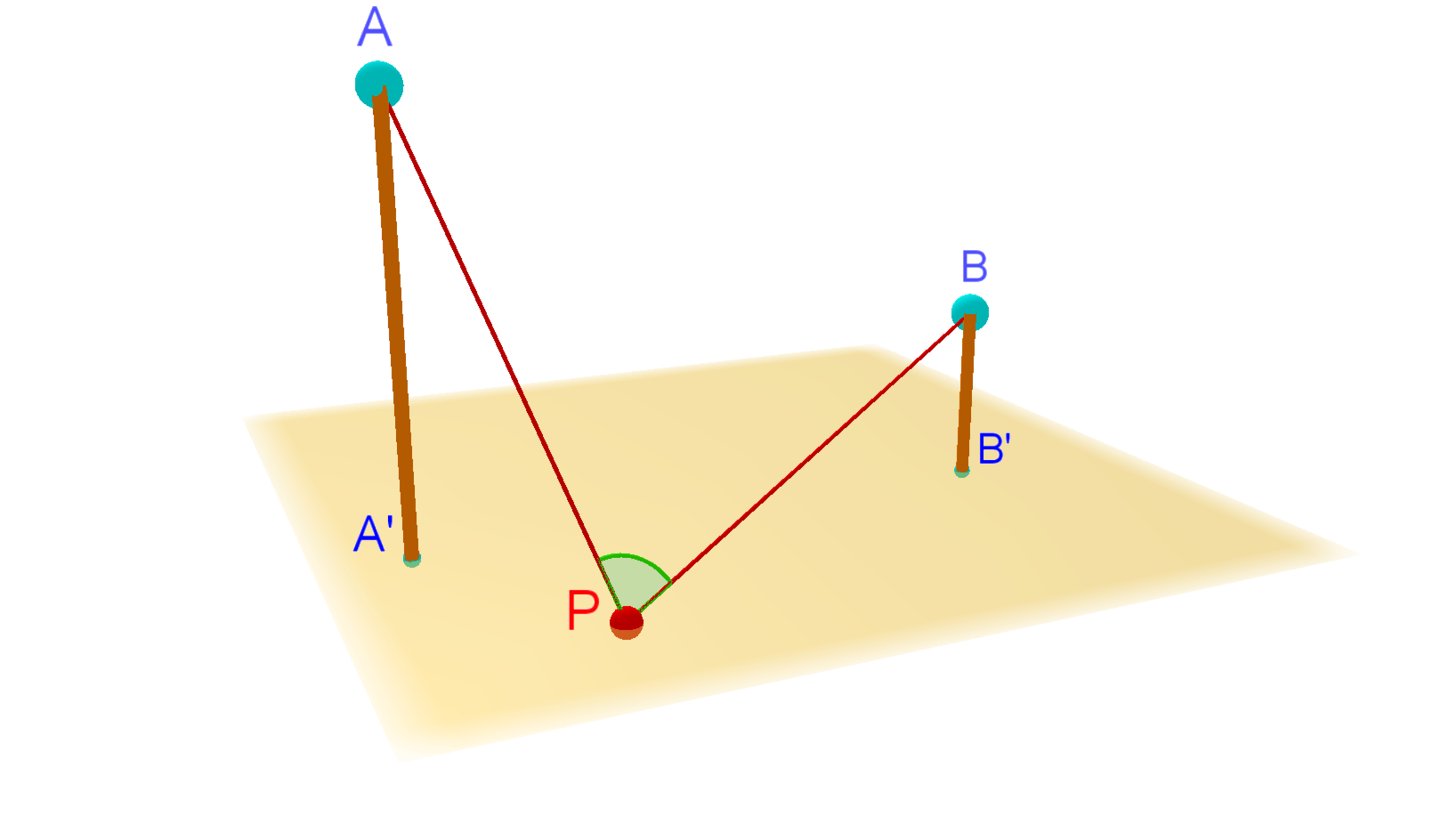
Two vertical poles stand 8 . 4 m apart. A A ′ is 4 . 4 m high, B B ′ is 3 . 1 m high. A point P on the ground is defined to be a “convenient point”, if the viewing angle of points A and B from P is an acute one. If you move away from the poles, you can certainly find convenient points. There is a region of points on the ground, however, where all points are inconvenient .
If the area of this region of inconvenient points is k π m 2 for some integer k , find k .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I still don't understand, the angle should be obtuse inside the sphere, right on the surface and acute everywhere else.
Oh, we were looking at the inconvenient area
Log in to reply
Yep, the area where the angle is obtuse. (The "convenient" area is infinite.)
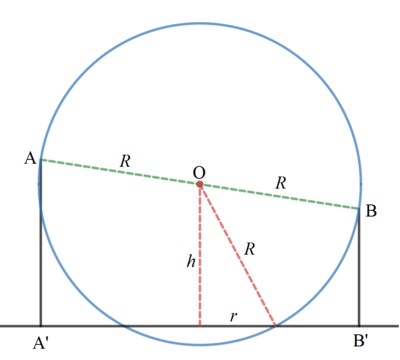
This region of inconvenient points in 3-D space is a sphere where the line A B is an axis through the center of the sphere. Therefore the radius of the sphere R = 2 8 . 4 2 + ( 4 . 4 − 3 . 1 ) 2 = 4 . 2 5 m . The center O of the sphere is horizontally midway between the two poles and h = 2 4 . 4 + 3 . 1 = 3 . 7 5 m above the ground. The portion of the sphere underground would have a top radius of r = R 2 − h 2 = 4 . 2 5 2 − 3 . 7 5 2 = 2 m .
Therefore the area of the inconvenient region is π r 2 = 4 π ⟹ k = 4 .
Let A ′ be ( 0 , 0 , 0 ) , A be ( 0 , 0 , 4 . 4 ) , B ′ be ( 8 . 4 , 0 , 0 ) , B be ( 8 . 4 , 0 , 3 . 1 ) , and P be ( x , y , 0 ) .
Now cos ∠ A P B = ∣ P A ∣ ∣ P A ∣ P A ⋅ P B ≤ cos 9 0 ° = 0 , so P A ⋅ P B ≤ 0 , or ( − x , − y , 4 . 4 ) ⋅ ( 8 . 4 − x , − y , 3 . 1 ) ≤ 0 , which rearranges to ( x − 4 . 2 ) 2 + y 2 ≤ 4 , a circle with a radius of 2 .
Therefore, the area of the region is 4 π , and k = 4 .
First note that inconvenient points are not limited to the ground.
Any point Q on the sphere with A B as diameter (apart from the points A , B themselves) subtends a right angle - that is, ∠ A Q B = 9 0 ∘ . This is the boundary of the set inconvenient points.
We want the area of the intersection of this sphere with the ground.
The sphere has radius R = 2 1 ( 4 . 4 − 3 . 1 ) 2 + 8 . 4 2 = 4 . 2 5
and its centre is at a height h = 2 4 . 4 + 3 . 1 = 3 . 7 5
The radius of the circular section made by the ground is then r = R 2 − h 2 = 2
and hence its area is 4 π .