Induction brake
A cart of mass is moving on a smooth surface with an initial velocity . On the cart is mounted a square coil with the cross-sectional area and number of turns . The coil is connected to a resistor with resistance . Now the cart enters a strong magnetic field, which increases linearly with the distance: where is the gradient of the field. As the coil enters the magnetic field, the cart is decelerated and finally comes to rest.
What distance has the car covered until it comes to a standstill?
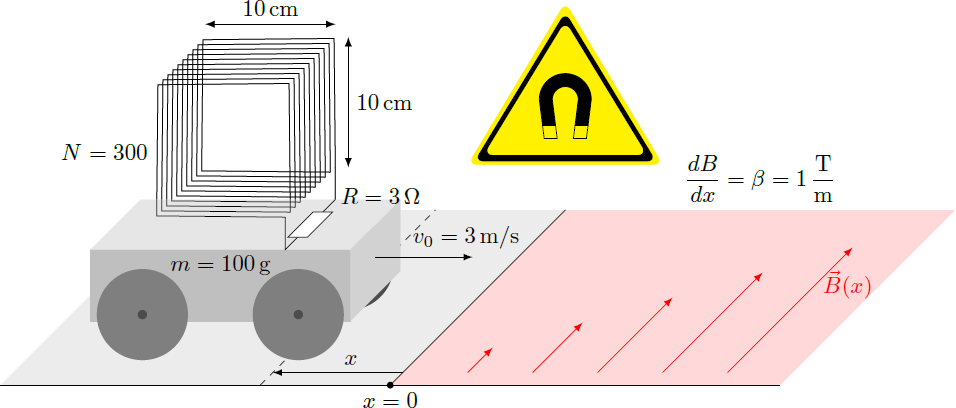
Details: We neglect the self-inductance of the coil, so that the induction voltage drops only at the resistance The electrical energy dissipated at the resistor corresponds to the loss of kinetic energy of the cart. The distance is measured from the right edge of the coil, so that for the magnetic field begins to penetrate into the coil.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We first calculate the induction voltage of the coil U = − d t d N ∫ B ( x ) ⋅ d A = − d t d N l ∫ x ( t ) − l x ( t ) B ( x ′ ) ⋅ d x ′ = − d t d N l { 2 1 β x ( t ) 2 β ( x ( t ) − l / 2 ) l x ( t ) < l x ( t ) ≥ l = { − N l β x ( t ) v ( t ) − N l 2 β v ( t ) x ( t ) < l x ( t ) ≥ l Due to the electrical resistance we get an electric current I = U / R and thus an electric power P = U I . The electric power comes from the loss of kinetic energy of the cart. Therefore, a decelerating force F = − F e x acts on the cart with P ⇒ F = R U 2 = F v = R v U 2 = { R ( N l β ) 2 x 2 v R ( N l 2 β ) 2 v x < l x ≥ l The equation of motion must be solved separately for the cases x < l and x ≥ l . In the first case, these can easily be integrated over time ⇒ ⇒ m d t d v m ( v − v 0 ) v 1 = v ( t 1 ) = − R ( N l β ) 2 x 2 v = − 3 R ( N l β ) 2 d t d ( x 3 ) = − 3 R ( N l β ) 2 x 3 = x = l v 0 − 3 m R ( N β ) 2 l 5 = ( 3 − 3 ⋅ 0 . 1 ⋅ 3 ( 3 0 0 ⋅ 1 ) 2 ⋅ ( 0 . 1 ) 5 ) s m = 2 s m where t 1 denotes the time when the car reaches the position x = l . Because of v 1 > 0 the car has not stopped yet, so we have to solve the equations of motion also for the case x > 0 . For this we use the separation of the variables: ⇒ ⇒ ⇒ m d t d v v d v ∫ v 1 v ( t ) v d v v ( t ) = − R ( N l 2 β ) 2 v = − τ d t , where τ : = ( N l 2 β ) 2 m R = 3 0 1 s = lo g v 1 v ( t ) = − τ t − t 1 = v 1 exp ( − τ t − t 1 ) , where t ≥ t 1 The entire distance covered then results through integration over time s = x ( t 1 ) + ∫ t 1 ∞ v ( t ) d t = l + [ − v 1 τ exp ( − τ t − t 1 ) ] t 1 ∞ = l + v 1 τ = ( 0 . 1 + 2 ⋅ 3 0 1 ) m ≈ 1 6 . 7 cm