Induction or function? (corrected)
Let f be a function from Z + to Z ∗ such that
- f ( 1 ) = 0
- f ( 2 n ) = 2 f ( n ) + 1
- f ( 2 n + 1 ) = 2 f ( n ) .
Find the smallest value of n such that f ( n ) = 1 9 9 4 .
Notation: Z + denotes the set of positive integers, and Z ∗ denotes the set of non-negative integers.
The answer is 2101.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Same solution here
I did same and checked with bruteforce https://repl.it/repls/UntidyHotpinkIrishsetter
Why?
You provide an algorithm without explaining why your algorithm should provide a correct solution.
Log in to reply
The reason is noted in the problem: The value of f ( 2 n + 1 ) is twice the value of f ( n ) , thus f ( 2 n + 1 ) ≡ 0 ( m o d 2 ) . In the same way, f ( 2 n ) ≡ 1 ( m o d 2 ) . That's why I did like that in my solution.
I think this comment may bring an appropriate account to my solution. Please comment if my explanaiton isn't enough.
Notice that: f ( 1 ) = 0 , f ( 2 ) = 1 , f ( 3 ) = 0 , f ( 4 ) = 3 , f ( 5 ) = 2 , f ( 6 ) = 1 ,
f ( 7 ) = 0 , f ( 8 ) = 7 . . . .
Using our imagination a bit, we claim that f ( 2 m + k ) = 2 m − k − 1 , for 0 ≤ k < 2 m − 1 . We'll proceed by induction.
Suppose f ( 2 m ) = 2 m − 1 , then
f ( 2 m + 1 ) = 2 f ( 2 m ) + 1 = 2 ( 2 m − 1 ) + 1 = 2 m + 1 − 1 ,
thus, our inductive assumption is correct for every power of 2 . Now, suppose our assumption is true for every number s ≤ 2 m + k , with 0 ≤ k < 2 m − 1 . Let's see what happens with s = 2 m + k + 1 . If k + 1 is even,
f ( 2 m + k + 1 ) = 2 f ( 2 m − 1 + 2 k + 1 ) + 1 =
2 ( 2 m − 1 − 2 k + 1 − 1 ) + 1 = 2 m − ( k + 1 ) − 1 .
If k + 1 is odd,
f ( 2 m + k + 1 ) = 2 f ( 2 m − 1 + 2 k ) = 2 ( 2 m − 1 − 2 k − 1 ) + 1 = 2 m − ( k + 1 ) − 1 ,
which proves our assumption.However, we want f ( n ) = 1 9 9 4 , so, we have to find m and k such that 2 m − k − 1 = 1 9 9 4 , or, k = 2 m − 1 9 9 5 . Then, the minimum value of n is obtained when m = 1 1 and k = 5 3 . The desired value is, thus, n = 2 1 1 + 5 3 = 2 1 0 1 .
Perfect induction proof! I recognized the pattern after calculating first 16 terms. And then I found the minimum power of 2 that is larger than 1994 ( it is 11 ) and the required shift in n to the right from 2048. The shift is 2047-1994 = 53, so n = 2048 + 53 = 2101. Thanks for the proof!
We claim the following: if we represent n in binary without any leading 0, then f ( n ) is obtained by swapping all 0's to 1's and vice versa (and removing all initial 0's caused). The proof is by strong induction. The base case f ( 1 ) = 0 is given, so let's assume it has been proven for all n < k and we want to prove it for n = k . Suppose k = 2 p + q where p ∈ N and q ∈ { 0 , 1 } (exists by division algorithm). Then f ( k ) = 2 f ( p ) + ( 1 − q ) . Observe that in binary, 2 f ( p ) + ( 1 − q ) is obtained by writing f ( p ) in binary, followed by one additional digit 1 − q . By our strong induction used on n = p (valid because p ≤ 2 k < k ), f ( p ) is the binary digits of p flipped (0's swapped with 1's), and 1 − q is q flipped. This means f ( k ) is exactly writing out the digits of p flipped, followed by q flipped. But this is simply writing out the digits of k flipped. This proves the claim.
Now since 1 9 9 4 = 1 1 1 1 1 0 0 1 0 1 0 2 , our desired n must be in the form … 0 0 0 0 0 1 1 0 1 0 1 2 . However, the ellipsis part cannot be zero; if it is, then n = 1 1 0 1 0 1 2 and f ( n ) = 0 0 1 0 1 0 2 instead. So the ellipsis part must be at least 1, giving 1 0 0 0 0 0 1 1 0 1 0 1 2 = 2 1 0 1 which is indeed a solution.
Induction by binary structure of n
Any positive integer n can be written uniquely in binary expansion, n = a 0 + 2 a 1 + 4 a 2 + ⋯ + 2 k a k + ⋯ + 2 d − 1 a d − 1 + 2 d , a i ∈ { 0 , 1 } . This is equivalent to the calculation 1 ↦ × 2 + a d − 1 ⋅ ↦ × 2 + a d − 2 ⋯ ↦ × 2 + a 0 n . The recursion relations of f show that f ( k × 2 + a ) = f ( k ) × 2 + ( 1 − a ) , so that we get 1 ↦ × 2 + 1 − a d − 1 ⋅ ↦ × 2 + 1 − a d − 2 ⋯ ↦ × 2 + 1 − a 0 f ( n ) . This translates to f ( n ) = ( 1 − a 0 ) + 2 ( 1 − a 1 ) + 4 ( 1 − a 2 ) + ⋯ + 2 d − 1 ( 1 − a d − 1 + 2 d ⋅ 0 ) = ( 1 + 2 + 4 + ⋯ 2 d ) − ( a 0 + 2 a 1 + 4 a 2 + ⋯ + 2 d − 1 a d − 1 + 2 d ) = 2 d + 1 − 1 − n . Since n ≥ 2 d , it follows that f ( n ) < 2 d . Conversely, n = 2 d + 1 − 1 − f ( n ) . Here, d is any number with the property f ( n ) < 2 d .
Apply this to f ( n ) = 1 9 9 4 . Since 2 1 0 < 1 9 9 4 < 2 1 1 , we need d = 1 1 at least. With this choice, n = 2 1 2 − 1 − 1 9 9 4 = 4 0 9 5 − 1 9 9 4 = 2 1 0 1 .
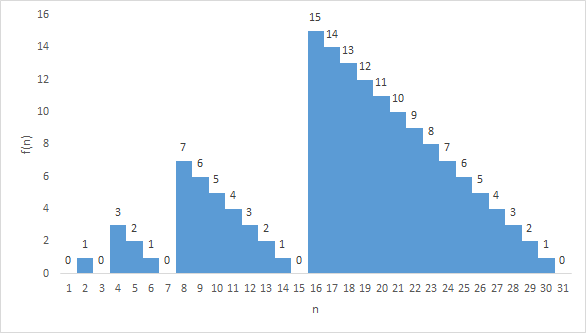 The function is an increasing saw function as shown in the figure. The maxima of
f
(
n
)
occur when
n
are powers of 2 and
f
(
2
k
)
=
2
k
−
1
, then
f
(
n
)
decreases by 1 as
n
increases by 1, such that
f
(
2
k
+
j
)
=
2
k
−
1
−
j
, until when
n
=
2
k
+
1
−
1
or
j
=
2
k
−
1
when
f
(
2
k
+
1
−
1
)
=
0
. Next then
f
(
2
k
+
1
)
=
2
k
+
1
−
1
.
The function is an increasing saw function as shown in the figure. The maxima of
f
(
n
)
occur when
n
are powers of 2 and
f
(
2
k
)
=
2
k
−
1
, then
f
(
n
)
decreases by 1 as
n
increases by 1, such that
f
(
2
k
+
j
)
=
2
k
−
1
−
j
, until when
n
=
2
k
+
1
−
1
or
j
=
2
k
−
1
when
f
(
2
k
+
1
−
1
)
=
0
. Next then
f
(
2
k
+
1
)
=
2
k
+
1
−
1
.
Let us first prove f ( 2 k ) = 2 k − 1 for all k ≥ 1 by induction. For k = 1 , f ( 2 ) = 1 = 2 1 − 1 , hence the claim is true. Assuming the claim is true for k , then f ( 2 k + 1 ) = f ( 2 ⋅ 2 k ) = 2 f ( 2 k ) + 1 = 2 ( 2 k − 1 ) + 1 = 2 k + 1 − 1 . Therefore, the claim is also true for k + 1 , hence true for all k ≥ 1 .
From f ( 2 n + 1 ) = 2 f ( n ) = f ( 2 n ) − 1 . This means that f ( m + 1 ) = f ( m ) − 1 , if m is even. Now consider, f ( 2 ( 2 n ) ) = 2 f ( 2 n ) + 1 , ⟹ f ( 2 ( 2 n ) + 1 ) = 2 f ( 2 n ) . And f ( 2 ( 2 n + 1 ) ) = 2 f ( 2 n + 1 ) + 1 = 2 f ( 2 n ) − 1 , ⟹ f ( 4 n + 2 ) = f ( 4 n + 1 ) − 1 . ⟹ f ( m + 1 ) = f ( m ) − 1 , if m is odd. Therefore,
{ f ( n ) = n − 1 f ( n + 1 ) = f ( n ) − 1 if n = 2 k , where k ∈ N if n = 2 k ⟹ f ( n ) = 2 ⌊ lo g 2 n ⌋ − 1 − ( n − 2 ⌊ lo g 2 n ⌋ ) = 2 ⌊ lo g 2 n ⌋ + 1 − n − 1
This implies that if f ( n ) = N , ⟹ n = 2 k − 1 + ( 2 k − N ) = 2 k + 1 − N − 1 , where k = ⌈ lo g 2 N ⌉ . Therefore for N = 1 9 9 4 , k = 1 1 and n = 4 0 9 6 − 1 9 9 4 − 1 = 2 1 0 1 .
We write 1 9 9 4 = 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ 7 + 1 ) + 1 ) ) ) + 1 ) ) + 1 ) . It's easily to find that 8 is the smallest number such that f ( 8 ) = 7 . Using the definition of f as well as the backward substitution, we have 1 9 9 4 = 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ f ( 8 ) + 1 ) + 1 ) ) ) + 1 ) ) + 1 ) = 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ ( 2 ⋅ f ( 1 6 ) + 1 ) ) ) + 1 ) ) + 1 ) = ⋯ = f ( 2 1 0 1 ) .
Although some programs have already been posted, here is a short implementation of this function (Python):
1 |
|
This basically defines a recursive lambda-function that returns 0 if n is 1 (to avoid booleans – which are subclasses of integers anyway – I used the bitwise complement of the negative of n to check if it is 1 , that is − ( − n − 1 ) , which only evaluates to 0 , a falsy value, if n is 1 ). Then, if n is odd, then the function returns 2 f ( ⌊ 2 n − 1 ⌋ ) , otherwise 1 + 2 f ( ⌊ 2 n ⌋ ) . Because we check the parity of n , the ⌊ ⋅ ⌋ aren't even required, but I included them anyway because that's what my program does.
To see the smallest integer n that satisfies the condition f ( n ) = 1 9 9 4 , you can simply run the following snippet after defining the above function:
1 2 3 |
|
Of course, this implementation yields our correct result, 2101 .
Here's a C program to compute the answer...
/* File: Br.c
Compile with: gcc Br.c -O3 -o Brill
Run with: ./Brill
Output: n = 2101 gives f(n) = 1994
*/
#include<stdio.h>
int f(int);
int main() {
int n = 0, ans = 0;
while(ans != 1994) {
n++;
ans = f(n);
}
printf("n = %d gives f(n) = %d\n", n, ans);
return 0;
}
int f(int n) {
if(n==1) {
return 0;
} else if(n%2 == 0) {
return 2 * f(n/2) + 1;
} else {
return 2 * f( (n-1) / 2);
}
}
Nice solution. Jerry has a programming solution that does not involve explicit recursion, by the way.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
1 |
|
{1: 0, 2: 1, 3: 0, 4: 3, 5: 2, 6: 1, 7: 0, 8: 7, 9: 6, 10: 5, 11: 4, 12: 3, 13: 2, 14: 1, 15: 0, 16: 15, 17: 14, 18: 13, 19: 12, 20: 11, 21: 10, 22: 9, 23: 8, 24: 7, 25: 6, 26: 5, 27: 4, 28: 3, 29: 2, .................................................... , 2008: 39, 2009: 38, 2010: 37, 2011: 36, 2012: 35, 2013: 34, 2014: 33, 2015: 32, 2016: 31, 2017: 30, 2018: 29, 2019: 28, 2020: 27, 2021: 26, 2022: 25, 2023: 24, 2024: 23, 2025: 22, 2026: 21, 2027: 20, 2028: 19, 2029: 18, 2030: 17, 2031: 16, 2032: 15, 2033: 14, 2034: 13, 2035: 12, 2036: 11, 2037: 10, 2038: 9, 2039: 8, 2040: 7, 2041: 6, 2042: 5, 2043: 4, 2044: 3, 2045: 2, 2046: 1, 2047: 0, 2048: 2047, 2049: 2046, 2050: 2045, 2051: 2044, 2052: 2043, 2053: 2042, 2054: 2041, 2055: 2040, 2056: 2039, 2057: 2038, 2058: 2037, 2059: 2036, 2060: 2035, 2061: 2034, 2062: 2033, 2063: 2032, 2064: 2031, 2065: 2030, 2066: 2029, 2067: 2028, 2068: 2027, 2069: 2026, 2070: 2025, 2071: 2024, 2072: 2023, 2073: 2022, 2074: 2021, 2075: 2020, 2076: 2019, 2077: 2018, 2078: 2017, 2079: 2016, 2080: 2015, 2081: 2014, 2082: 2013, 2083: 2012, 2084: 2011, 2085: 2010, 2086: 2009, 2087: 2008, 2088: 2007, 2089: 2006, 2090: 2005, 2091: 2004, 2092: 2003, 2093: 2002, 2094: 2001, 2095: 2000, 2096: 1999, 2097: 1998, 2098: 1997, 2099: 1996, 2100: 1995, 2101: 1994}
f(1)=0 f(2)=1 f(3)=0 f(4)=3 f(5)=2 f(6)=1 f(7)=0 f(8)=7 f(9)=6
We can see that : For every natural r > 0 and natural a in range [0; 2^r[
n= 2^r+a
F(2^r + a) = 2^r - (a+1)
1994=2048-53=2^11-54= 2^r - (53 + 1)
So n=2^11=2048+53=2101
Here is my Brute solution to this problem:
Given:
f ( 1 ) = 0 , f ( 2 n ) = 2 f ( n ) + 1 ; f ( 2 n + 1 ) = 2 f ( n ) ;
Where n∈N,f(n)∈Z*,Notice that 2n is even while 2f(n)+1 is odd, and 2n+1 is odd while 2f(n) is even;
We can rewrite this function as:
f ( 1 ) = 0 ; f ( n ) = 2 f ( n / 2 ) + 1 , n = 2 k , k ∈ N ; f ( n ) = 2 f ( ( n − 1 ) / 2 ) , n = 2 k + 1 , k ∈ N ;
Since f(n)=1994,1994 is even,
thus 2f((n-1)/2)=1994,
f((n-1)/2)=997,
let n1=(n-1)/2,f(n1)=997;
Since 997 is odd,
2f(n1/2)+1=997;
thus f(n1/2)=498,
let n2=n1/2,
f(n2)=498,
.........And so on.
Until we find f(n11)=0;
Since we are finding the smallest n,even if there are multiple n11∈N such that f(n11)=0,we take the smallest value,thus n11=1;
And we are going all the way back:
n11=n10/2,
thus n10=2n11=2;
n10=n9/2,
n9=2n10=4;
n9=n8/2,
n8=2n9=8;
n8=n7/2,
n7=2n8=16;
n7=n6/2,
n6=2n7=32;
n6=(n5-1)/2,
n5=2n6+1=65;
............
Until we get n1=1050,
Since n1=(n-1)/2,
Thus n=2101;
And finally we are done.
Although it's a method that needs least consideration,but it would drive you crazy if you are dealing with bigger numbers by hand.
It's better to use a calculator or program when using this method.
A python solution
1 2 3 4 5 6 7 8 9 10 11 |
|
When you use
x.index(n/2)
, the list
x
is scanned linearly to search for
n/2
. Is there a way we can perform better?
Log in to reply
I would have to explore the function better. There probably is a way to know what the exact index on the previous recursion is, but I didn't go in to that much detail in my coding.
1994=997.2 997=2.498+1 498=2.249 249=2.124+1 124=2.62 62=2.31 31=15.2+1 15=7.2+1 7=3.2+1 3=2.1+1
F(2)=2.0+1 F(4)=2.1+1 F(8)=2.3+1 F(16)=15 F(32)=31 F(65)=62 F(131)=124 F(262)=249 F(525)=498 F(1050)=997 F(2101)=1994
Did you calculate all of these values by hand?

Let's divide 1 9 9 4 by 2 consecutively, selecting only quotients.
1 9 9 4 , 9 9 7 , 4 9 8 , 2 4 9 , 1 2 4 , 6 2 , 3 1 , 1 5 , 7 , 3 , 1 , 0 .
Then, determine n to the numbers repectively: 1 , 2 , 4 , 8 , 1 6 , 3 2 , 6 5 , 1 3 1 , 2 6 2 , 5 2 5 , 1 0 5 0 , and 2 1 0 1 .
Thus, the answer is 2 1 0 1 .