Inductive Source?
The switch closes at time , and the inductor is de-energized prior to closing.
At time , what fraction of the instantaneous power consumed by the resistor is supplied by the inductor?
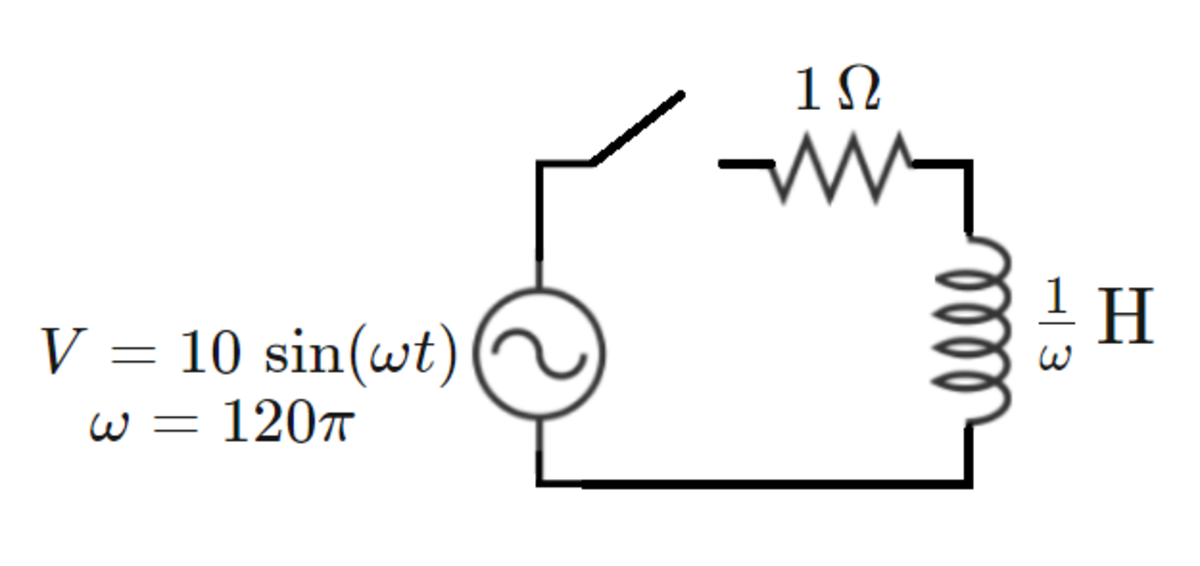
The answer is 0.785.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the Laplace transform, we have
I ( s ) = ( s 2 + ω 2 ) ( ω s + 1 ) 1 0 ω = ( s 2 + ω 2 ) ( s + ω ) 1 0 ω 2
By partial fractions, this becomes
I ( s ) = ( s + ω ) A + s 2 + ω 2 B s + C
Multiplying left and right by ( s + ω ) ( s 2 + ω 2 ) yields,
1 0 ω 2 = A ( s 2 + ω 2 ) + ( B s + C ) ( s + ω )
Equating the coefficients of the powers of s on both sides of the equation, yields,
A + B = 0
B ω + C = 0
A ω 2 + C ω = 1 0 ω 2
And this linear system solves to A = 5 , B = − 5 , C = 5 ω , so that
I ( s ) = s + ω 5 + s 2 + ω 2 − 5 s + 5 ω
Taking the inverse Laplace transform, we get,
i ( t ) = 5 e − ω t − 5 cos ω t + 5 sin ω t
Now the instantaneous power through the resistor is
p ( t ) = v ( t ) i ( t ) = R i 2 ( t ) = i 2 ( t )
And the power supplied by the source is
p S ( t ) = V S ( t ) i ( t ) = ( 1 0 sin ω t ) i ( t )
So that the power supplied by the inductor is
p L ( t ) = p ( t ) − p S ( t )
Plugging in ω = 1 2 0 π and t = 0 . 0 0 8 , gives p = 3 4 . 0 1 5 0 3 6 8 6 and p S = 7 . 3 0 9 7 3 6 4 2 6 , and hence, the required fraction is
Fraction of powers = p p − p S = 0 . 7 8 5