Inelastic collision
Two equal discs initially at rest are in contact on a smooth table. A third disc of same mass but of double radius strikes them symmetrically and itself comes to rest after impact.
The coefficient of restitution is =
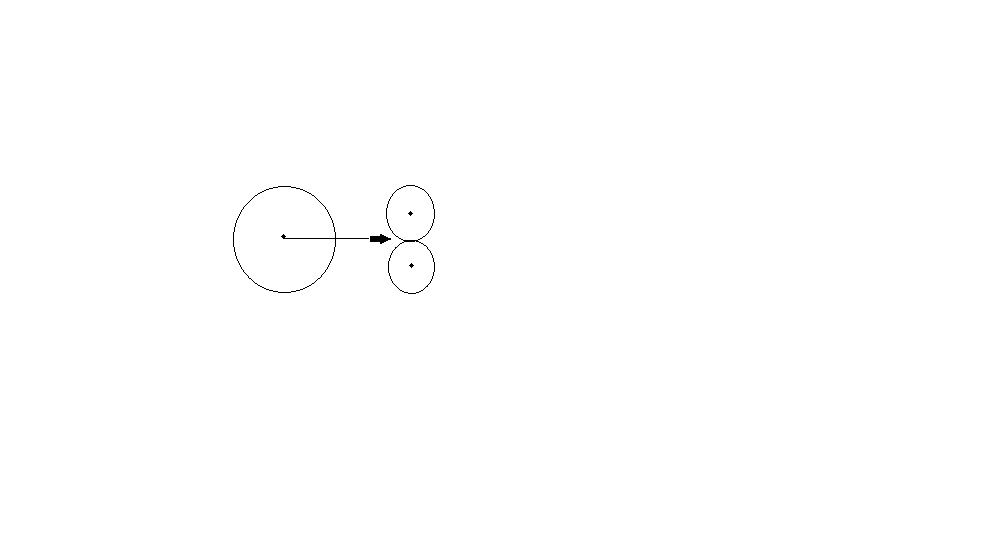
The answer is 0.5625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the velocity of the bigger ball be v 0 , depicted in the problem, and v be the velocity of smaller balls. After collision, the smaller balls move along the line of impact, depicted in the figure.
Conserving momentum along the X − axis, we get: m v 0 = 2 m v cos θ or v 0 = 2 v cos θ
Coefficient of restitution, e , is defined as the Ratio of velocity of separation and velocity of approach, along the line of impact.
Therefore, e = v 0 cos θ v
From the diagram, we can easily deduce that cos θ = 3 2 2 .
Solving from the above three, we get e = 1 6 9 .