Inellipse of a triangle
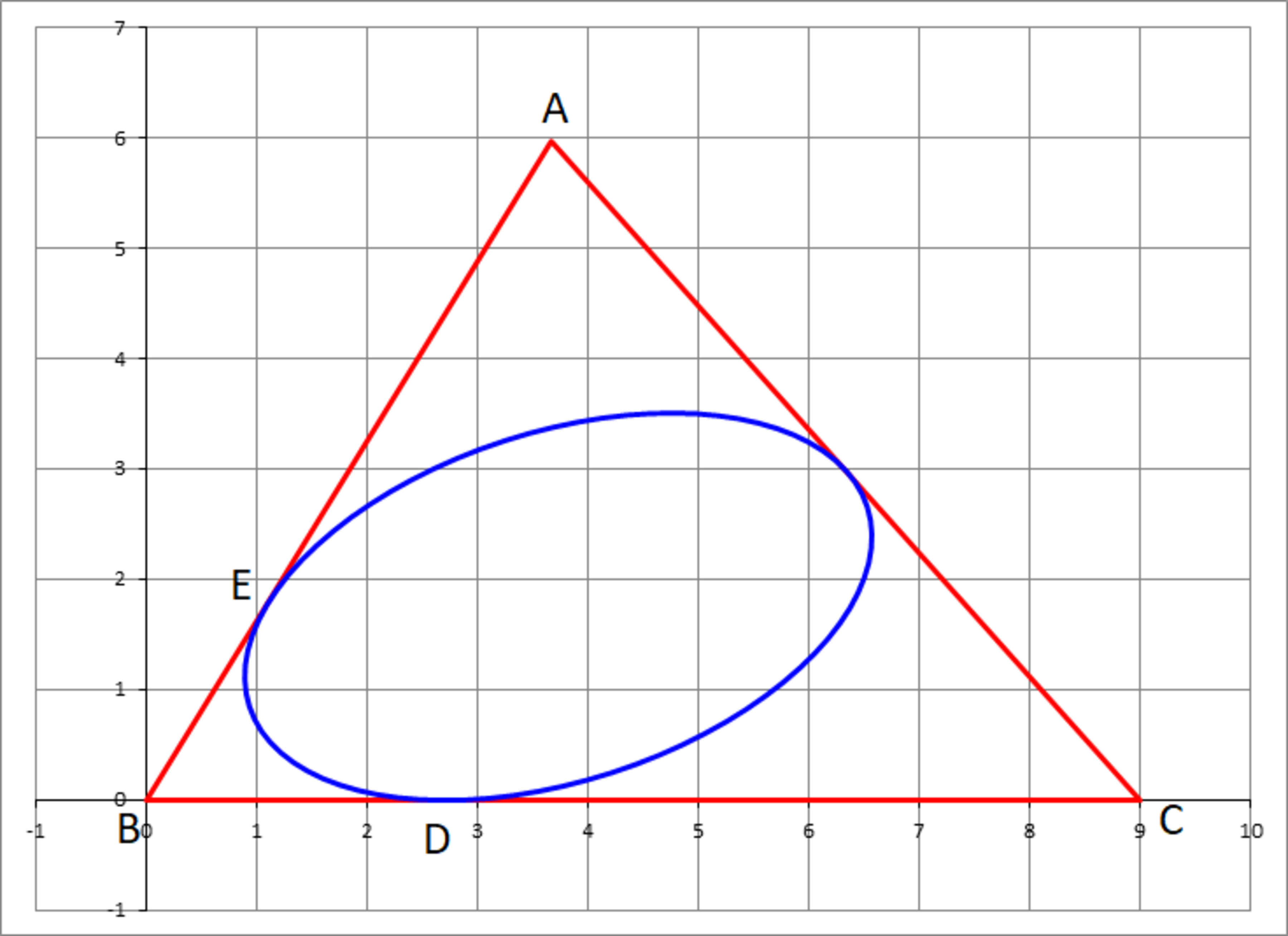
has . We want to draw the inellipse that is tangent to side at point , where , and also tangent to side at point where . If the center of this inellipse is and the lengths of its semi-major and semi-minor axes are and , then find the sum .
The answer is 9.997.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If B is ( 0 , 0 ) and C is ( 9 , 0 ) (as pictured), and A is ( A x , A y ) , then by the distance equation:
A B = ( A x − 0 ) 2 + ( A y − 0 ) 2 = 7
A C = ( A x − 9 ) 2 + ( A y − 0 ) 2 = 8
which solves to A x = 3 1 1 and A y = 3 8 5 .
Since B E = 0 . 3 A B and B is at ( 0 , 0 ) and A is at ( 3 1 1 , 3 8 5 ) , the coordinates of E are ( 0 . 3 ⋅ 3 1 1 , 0 . 3 ⋅ 3 8 5 ) = ( 1 0 1 1 , 5 4 5 ) .
Since B D = 0 . 3 B C and B is at ( 0 , 0 ) and C is at ( 9 , 0 ) , the coordinates of D are ( 0 . 3 ⋅ 9 , 0 . 3 ⋅ 0 ) = ( 1 0 2 7 , 0 ) .
Using the equations from the link provided in the question, the points of contact are ( u 1 , u 2 ) = ( 1 0 2 7 , 0 ) and ( v 1 , v 2 ) = ( 1 0 1 1 , 5 4 5 ) , and s = t = 0 . 3 . That means:
a = s − 1 1 = 0 . 3 − 1 1 = − 7 1 0
b = t − 1 1 = 0 . 3 − 1 1 = − 7 1 0
the center of the inellipse is:
G ( x 0 , y 0 ) = M = a b − 1 a b ( 2 u 1 + v 1 , 2 u 2 + v 2 ) = ( 5 1 1 9 0 , 5 1 4 0 5 )
and the conjugate half-diameters of the ellipse are:
f 1 = 2 1 a b − 1 a b ( u 1 + v 1 , u 2 + v 2 ) = ( 5 1 1 3 3 , 5 1 2 8 5 )
f 2 = 2 1 a b − 1 a b ( u 1 − v 1 , u 2 − v 2 ) = ( 5 1 8 5 1 , − 5 1 4 2 5 5 )
Using the equation for the semi-axes lengths derived from this question :
a = 2 1 ( f 1 x 2 + f 1 y 2 + f 2 x 2 + f 2 y 2 ) + 2 1 ( ( f 1 x − f 2 y ) 2 + ( f 1 y + f 2 x ) 2 ) ( ( f 1 x + f 2 y ) 2 + ( f 1 y − f 2 x ) 2 ) = 5 7 8 3 2 1 7 + 3 1 5 1 9 6 9
b = 2 1 ( f 1 x 2 + f 1 y 2 + f 2 x 2 + f 2 y 2 ) − 2 1 ( ( f 1 x − f 2 y ) 2 + ( f 1 y + f 2 x ) 2 ) ( ( f 1 x + f 2 y ) 2 + ( f 1 y − f 2 x ) 2 ) = 5 7 8 3 2 1 7 − 3 1 5 1 9 6 9
Therefore, x 0 + y 0 + a + b = 5 1 1 9 0 + 5 1 4 0 5 + 5 7 8 3 2 1 7 + 3 1 5 1 9 6 9 + 5 7 8 3 2 1 7 − 3 1 5 1 9 6 9 = 5 1 1 9 0 + 4 0 5 + 3 3 2 1 7 + 1 6 8 2 5 5 ≈ 9 . 9 9 7 .