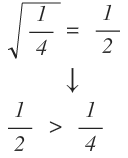Inequalities With Radicals

False because, for example:

The inequality $\sqrt x < x$ only holds true for real values $x>1$

Eg. $x=4 \implies \sqrt x = \sqrt4 = 2 < 4$

If $x=1$ or $x=0$ , we have $\sqrt x = x$ :

$x=1\implies \sqrt x = \sqrt 1 = 1 = x$

$x=0\implies \sqrt x = \sqrt 0 = 0 = x$

And for real values $0<x<1$ , the inequality becomes $\sqrt x > x$

Eg. $x=0.01\implies \sqrt x = \sqrt {0.01} = 0.1 > 0.01$

Lastly, for real values $x<0$ , we will get a complex value for its square root

Eg. $x=-4\implies \sqrt x = \sqrt {-4} = \sqrt{-1}\sqrt{4} = 2i$

Now, I do not know whether we can compare complex values with real values or not. Hopefully, someone else will answer this question.

Even without considering real values $x<0$ , we already have sufficient evidence to prove that $\sqrt x < x$ does not hold true for all real $x$ .

Thus, the answer is $\boxed{\text{False}}$

The inequality is false for all real $x \le 1$