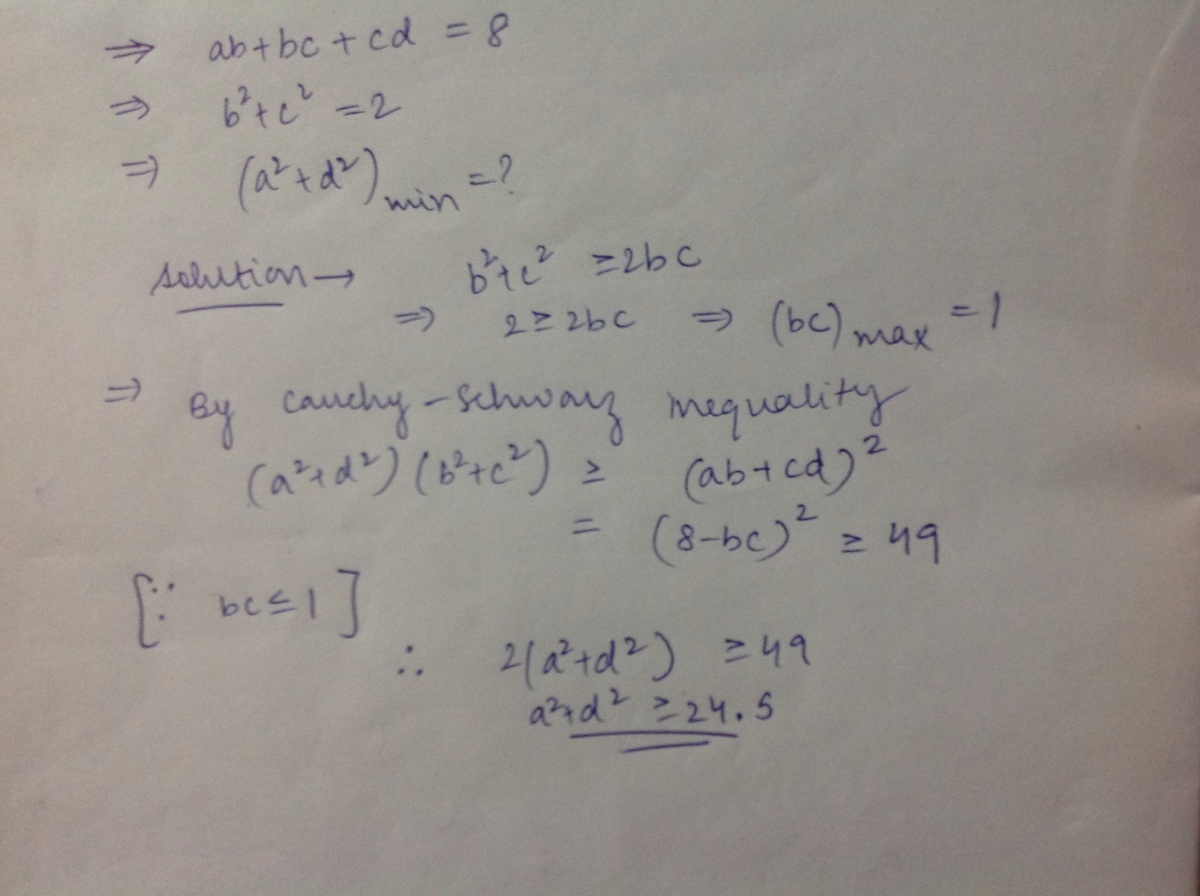Inequality Mania

My solution is using the Cauchy-schwarz inequality.

Let's first guess what the answer should be like. It is most likely that we have $b = c$ , in which case $b^2 + c^2 = 2 \Rightarrow b=c=1$ . Then, we have $a + 1 + d = 8$ , and so the minimum value of $a^2 + d^2$ occurs at $a = d = \frac{7}{2}$ .

Now, let's justify that this is indeed the correct answer.

We have $(2a-7b)^2 + 14 ( b-c)^2 + (7c-2d)^2 \geq 0$ , or that

$4 (a^2 + d^2) + 63 (b^2 + c^2 ) \geq 28 (ab + bc + cd) = 224$

Thus, $a^2 + d^2 \geq \frac{ 224 - 63 \times 2 } {4} = 24.5$ .

We verify that equality can occur with $a = d = \frac{7}{2}, b = c = 1$ .

Setting

$\left\{b=\sqrt{2} \cos (t),c=\sqrt{2} \sin (t)\right\}$

$\left\{\sin (x)=\frac{a}{\sqrt{a^2+d^2}},\cos (x)=\frac{d}{\sqrt{a^2+d^2}}\right\}$

a b+b c+c d = 8 becomes

$\sqrt{2} \sqrt{a^2+d^2} \sin (t+x)+\sin (2 t)=8$

Hence,

$a^2+d^2==\frac{1}{2} (\sin (2 t)-8)^2 \csc ^2(t+x)\geq \frac{49}{2}$

Let $S=a^{2}+d^{2}$ then $S>= 2ad$ . From $b^{2}+c^{2}=2$ we get $1>=bc$ Now $8=<ab+1+cd => ab+cd>=7$ by squaring we get that this expression is bigger than 49. By Am-Gm that expression is also bigger than $4abcd => 4abcd=49=> 4ad>=4abcd=49 => 2S>=49$ thus $S>=\boxed{24.5}$

Let b=2^1/2 sinA and c=2^1/2cosA. a2^1/2 sinA+2sinAcosA +d2^1/2 cosA =8. a2^1/2 sinA +sin2A+d2^1/2 cosA =8.2^1/2(a sinA +dcosA)=8-sin2A . 8-sin2A<=2^1/2( (a^2 + d^2)^1/2).

sin2A is maximum 1 8-1<=2^1/2( (a^2 + d^2)^1/2).7/(2^1/2)<=( (a^2 + d^2)^1/2).Squaring both sides w get minimum value as 49/2=24.5.I dont know how to use the formatting guide.

To minimize $a$ and $d$ , we have to maximize $b$ and $c$ . With that, we reasonably assume that $b,c>0$ in which by parity, we conclude that all $a,b,c,d>0$ . Using AM-GM and the given equality that $b^2+c^2=2$ , we have $\sqrt{\frac{b^2+c^2}{2}}=\frac{b+c}{2}=1\Longrightarrow b+c=2$

Hence, $ab+b(2-b)+(2-b)d=8$ . Lets call this equation $1$ .

Now, AM-GM gives $\frac{\sqrt{a^2+d^2}}{2}\geq\frac{a+d}{2}$ . Hence, minimizing $\sqrt{a^2+d^2}$ , equality case yields $a=d$ . Substituting into equation $1$ yields

$ab+b(2-b)+a(2-b)=8\Rightarrow -b^2+2b+2a-8=0$

Solving $b$ as a quadratic assuming $a$ is constant gives $b=\frac{-2\pm\sqrt{4+8(a-4)}}{-2}$ . Maximize $b$ , so we take the $+$ value, which gives $b=1+\sqrt{2a-7}$ . Since $b=c$ , then $\sqrt{2a-7}=0\Rightarrow a=\frac{7}{2}=d$ . Finally $\min(a^2+d^2)=\frac{7}{2}^2+\frac{7}{2}^2=\boxed{24.5}$ .

(a-b)^2+(b-c)^2+(c-d)^2 >= 0

a^2+b^2+b^2+c^2+c^2+d^2-2ab-2bc-2cd >=0

a^2+d^2>=2(ab+2bc+cd )-2(b^2+c^2)

a^2+d^2>=12