Inequality of Denominators
Let a , b , c be positive reals. Let k be the largest possible real such that a 1 + b 1 + c 1 + a + b 1 + b + c 1 + c + a 1 ≥ a + b + c k
If k can be expressed as q p for relatively prime positive integers p , q , then find p + q .
Inequality of Numerators , the easier version of this inequality.
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I bet some people tried to use Cauchy Schwarz, and ended up with k = 1 2 . Cauchy Schwarz, in this case, isn't strong enough!
Log in to reply
Started with Cauchy schwarz, ended up wrong 2 times, and then hit upon more elegent method, Nice trap @Daniel Liu
Log in to reply
It wasn't intended to be a trap, but it just happened to exist :P
An easy way to check if your inequality is strong enough is to look at the equality case. Equality case of Cauchy is a 2 = b 2 = c 2 = ( a + b ) 2 = ( b + c ) 2 = ( c + a ) 2 which only has the solution ( a , b , c ) = ( 0 , 0 , 0 ) which is not allowed.
I did so at first.
I can't catch the equation after you multiply it with a+b+c than you simplify it. Could you write more detail about how you simplify it?
Log in to reply
( a + b + c ) ( ∑ a 1 + ∑ a + b 1 ) = ∑ a a + b + c + ∑ a + b a + b + c = ∑ a a + a b + c + ∑ a + b a + b + a + b c = 3 + ∑ a b + c + 3 + ∑ a + b c = 6 + ∑ a b + c + ∑ a + b c
better?
Where do the summations come from, and what are the summations of 1-infinity?
Very good question. I used Titu's lemma and ended up with 12.
yeah this was my first approach of solution
Put a=b=c=1 and get the damn answer. A wild guess that the equality would exist if all of them were equal. I know that that is no method, but we Indians somehow find a way.
Log in to reply
That's a common way to cheat inequalities: to just plug in a = b = c .
However, you didn't prove that it was the answer.
By AM-HM a 1 + b 1 + c 1 3 ≤ 3 a + b + c and a + b 1 + b + c 1 + c + a 1 3 ≤ 3 2 ( a + b + c ) .
So: ( a + b + c ) ( a 1 + b 1 + c 1 ) ≥ 9 and ( a + b + c ) ( a + b 1 + b + c 1 + a + c 1 ) ≥ 2 9 .
Adding gives k = 2 2 7 .
Equality is obtained iff a = b = c
Or...the sets {a,b,c} and { a 1 , b 1 , c 1 } are oppositely ordered so by rearrangement inequality:
3 = a a + b b + c c ≤ a b + b c + c a 3 = a a + b b + c c ≤ a c + b a + c c 3 = a a + b b + c c ≤ a a + b b + c c
Adding the three inequalities gives:
9 ≤ ( a + b + c ) ( a 1 + b 1 + c 1 )
Appying this inequality to the triple ( a + b , a + c , b + c ) gives:
9 ≤ 2 ( a + b + c ) ( a + b 1 + b + c 1 + a + c 1 )
Add and we get k = 2 2 7
Log in to reply
You could have just used Cauchy to directly get 9 ≤ ( a + b + c ) ( a 1 + b 1 + c 1 )
Ok,the solutions here are so creative. Maybe mine one is very poor but if you substitute a=b=c=1 since the value of k is independent of it. After simplifying , we get k is less than or equal to 27/2 where p= 27, q= 2 which adds upto 29. LOL.Not creative but time saving.
Here's my solution:
We shall normalize by assuming a + b + c = 1 . Then, the inequality reduces to c y c ∑ a 1 + c y c ∑ 1 − a 1 ≥ k now, let f ( x ) = x 1 + 1 − x 1 . Since f ( x ) a convex function, by Jensen's Inequality, we have f ( 3 a + b + c ) ≤ 3 f ( a ) + f ( b ) + f ( c ) \] so, f ( a ) + f ( b ) + f ( c ) ≥ 2 2 7 . But we also know that ∑ c y c a 1 + ∑ c y c 1 − a 1 = f ( a ) + f ( b ) + f ( c ) . And hence we have k = 2 2 7 , so p + q = 2 7 + 2 = 2 9
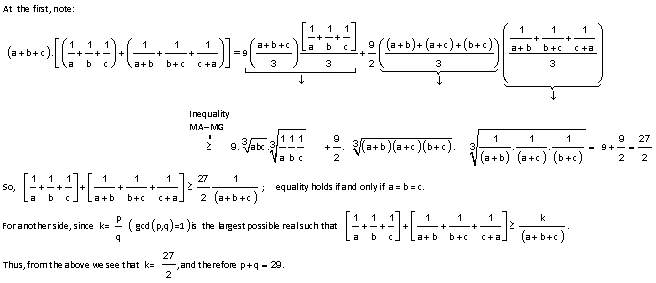
Multiply a + b + c on both sides and simplify to get 6 + ∑ c a + b + ∑ b + c a ≥ k
We see that ∑ c a + b = ∑ c a + c b ≥ 6 6 b a ⋅ a b ⋅ c a ⋅ a c ⋅ b c ⋅ c b = 6 by six-variable AM-GM.
Also, ∑ b + c a ≥ 2 3 by Nesbitt's Inequality.
So 6 + 6 + 2 3 ≥ k ⟹ k ≤ 2 2 7 and our answer is 2 7 + 2 = 2 9 .