Inequality with log

$\begin{aligned} \log_4 \log_3 \log_2 (x^2+7x) & \ge 0 \\ \implies \log_3 \log_2 (x^2+7x) & \ge 4^0 = 1 \\ \log_2 (x^2+7x) & \ge 3^1 \\ x^2+7x & \ge 2^3 \\ \implies x^2 + 7x - 8 & \ge 0 \\ (x+8)(x-1) & \ge 0 \\ \implies x & \in (-\infty, -8] \cup [1, \infty) \end{aligned}$

$\implies \dfrac ab = \boxed{-8}$

$\begin{aligned} \log_4 \log_3 \log_2 (x^2 + 7x) & \geq 0\\ \log_4 \log_3 \log_2 (x^2 + 7x) & \geq \log_4 \log_3 \log_2 2^3\\ x^2 + 7x & \geq 8\\ x^2 + 7x - 8 & \geq 0\\ (x + 8)(x - 1) & \geq 0\\ x & \in (-\infty, -8] \cup [1, \infty) \end{aligned}$

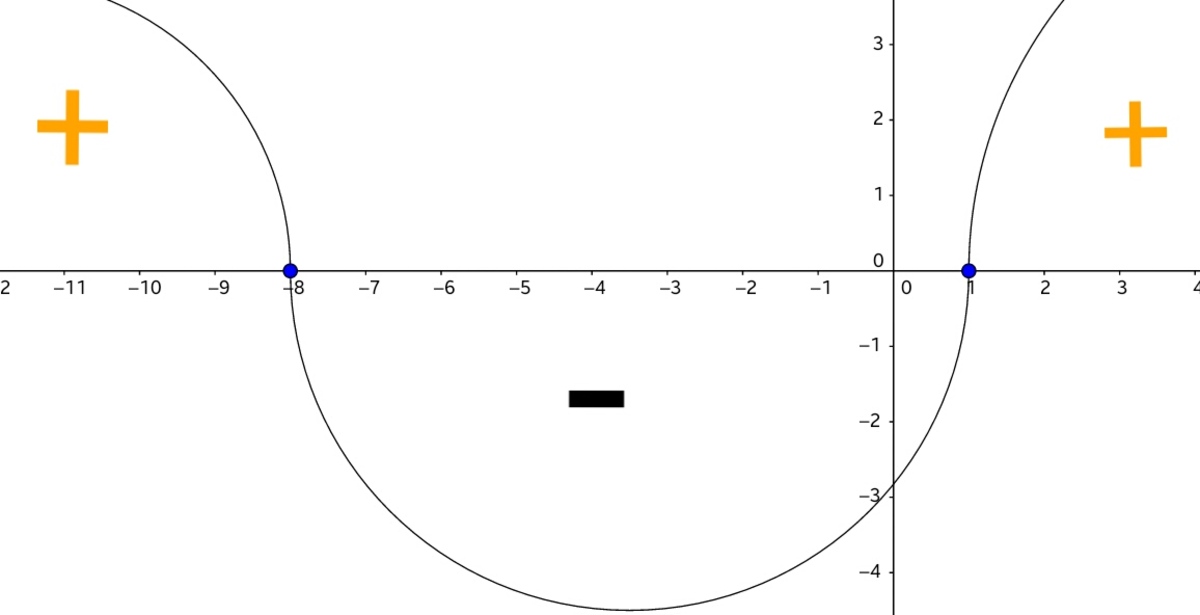
But we have to also check if the argument of the given expression is more than $0$ as it becomes negative in a contrary situation.

$\begin{aligned} x^2 + 7x & > 0\\ x(x + 7) & > 0\\ x & \in (-\infty, -7) \cup (0, \infty) \end{aligned}$

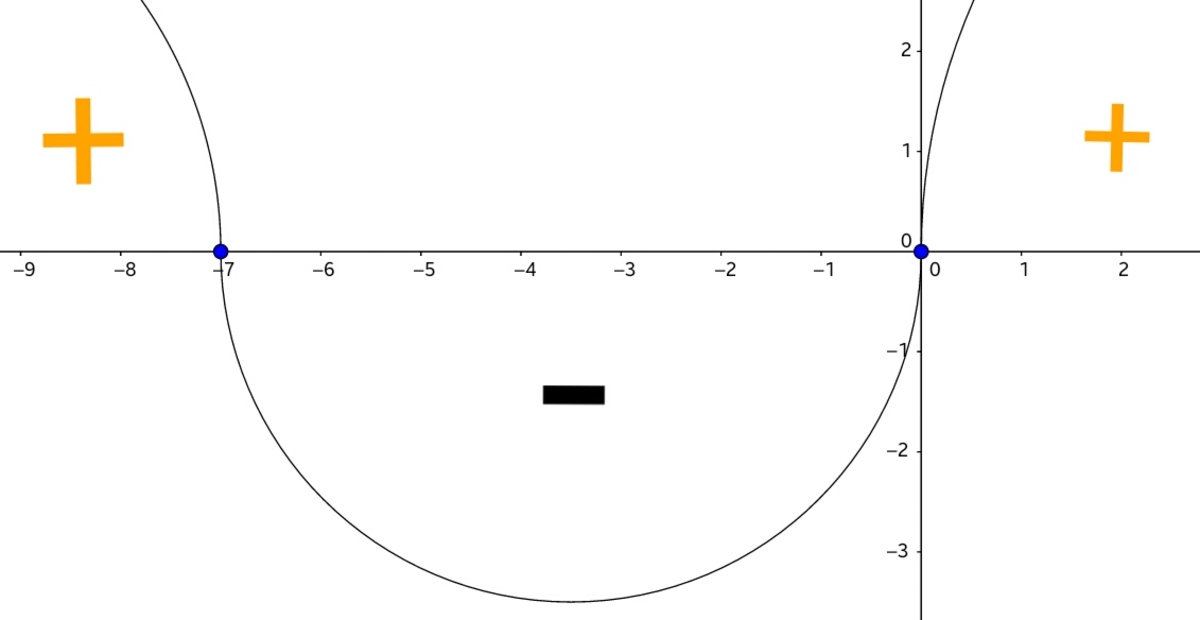
So, our final answer is $\color{#20A900}{\left[(-\infty , -8] \cup [1, \infty)\right]} \cap \color{#D61F06}{\left[(-\infty, -7) \cup (0, \infty)\right]}\\ = \color{#EC7300}{(-\infty, -8] \cup [1, \infty)}$

So, $\begin{aligned} \dfrac{a}{b} & = \dfrac{-8}{1}\\ & = \color{#3D99F6}{\boxed{-8.00}} \end{aligned}$