Inequality with product and division

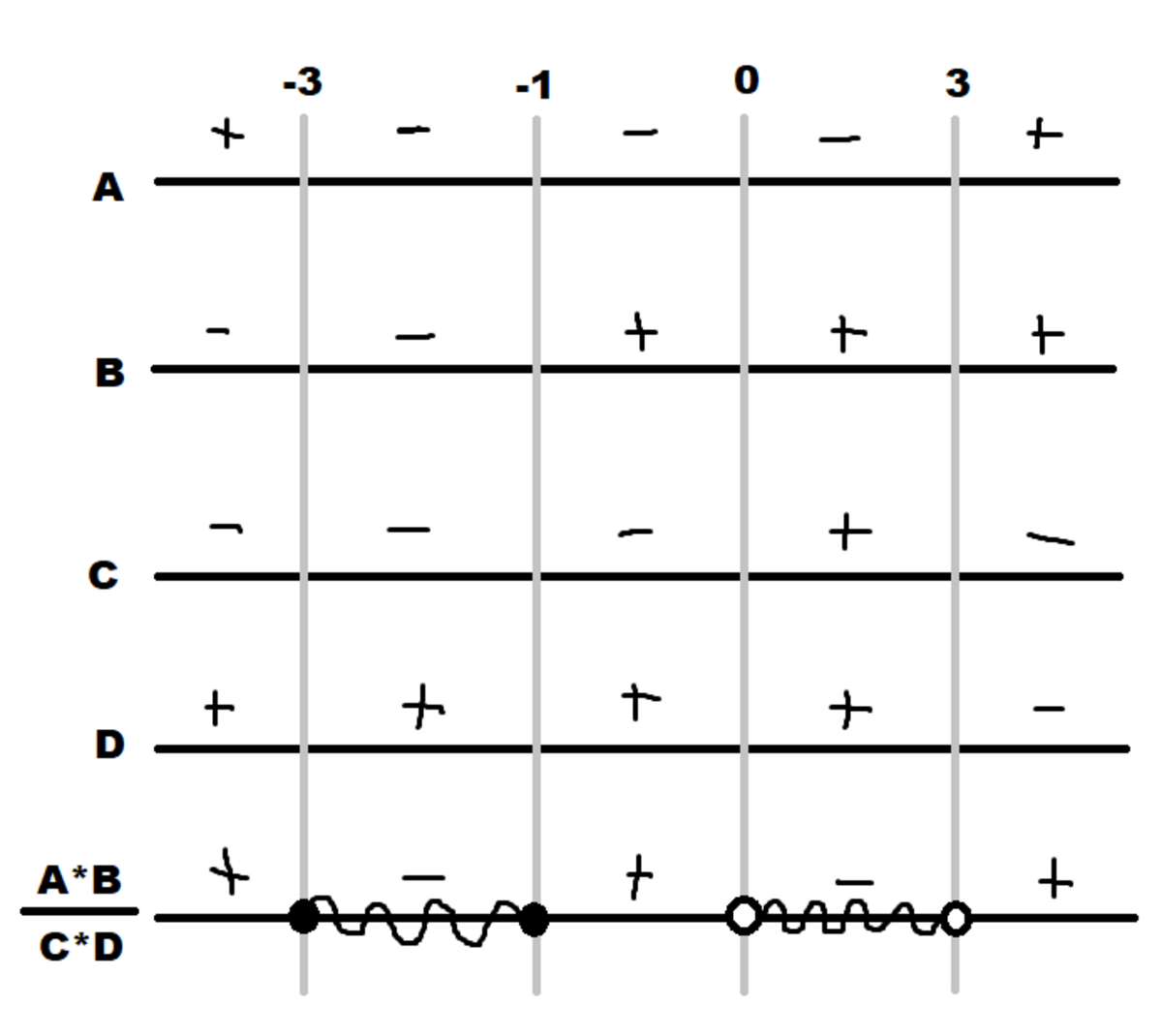
Step 1: Find when the numerator switches signs.

$(x^2 - 9)(2x + 2)$

$2(x - 3)(x + 3)(x + 1)$

The roots are -3, -1, and 3.

Since the leading coefficient is positive, as $x \rightarrow \infty, y \rightarrow \infty$

Since polynomial has a degree of 3, as $x \rightarrow \infty, y \rightarrow -\infty$ and the sign switches with each root.

Therefore the signs of values of x from -4 to 4 are:

Step 2: Find when the denominator switches signs.

$(-2x^2 + 6x)(-x + 3)$

$2x(x - 3)(x - 3)$

$2x(x - 3)^2$

The roots are 0 and 3 (second degree).

Since the leading coefficient is positive, as $x \rightarrow \infty, y \rightarrow \infty$

Since polynomial has a degree of 3, as $x \rightarrow \infty, y \rightarrow -\infty$ and the sign switches with each root except 3.

Therefore the signs of values of x from -4 to 4 are:

Step 3: Find when the numerator and denominator have different signs or when the numerator is zero and the denominator is nonzero.

Such values of x are -3, -2, -1, 1, and 2. The sum of these numbers is $\boxed{-3}$

What the question is asking is what integers makes the expression negative, and a good trick to solve this is to divide the expression into chunks and then solve each one for when they're equal to zero, in this case:

A = X^2-9 = (X-3)(X+3), so X=3 or X=-3

B = 2X+2, so X=-1

C = -2X^2+6X = X(-2X+6), so X=0 or X=3

D = -X+3, so X=3

Then look at the graphs of each equation and notice when they'll be positive, negative or equal to zero:

A) In this second degree equation, X^2 is being multiplied by 1, a positive number, so the parabola will cross the x-axis first from the positive area to the negative, and then from the negative area to the positive, and by knowing when the expression's goint to be zero, the graph and whether it'll be positive or negative will look like:

B) It's a first degree equation, and X is being multiplied by 2, a positive number, so the larger X is, larger the expression's value will be, so it'll look like:

C) It's a second degree equasion and X^2 is being multiplied by -2, a negative number, so it'll first cross the x-axis from the negative area to the positive and then from the positive area to the negative, so the graph will look like:

D) This is a first degree equasion which has X being multiplied by -1, a negative number, so the larger X is, the smaller the expression's value will be, so the graph will look like:

Now all we have to do is remember that two numbers with the same sign multiplied or divided is going to be positive and two numbers with different sign multiplied or divided is going to be negative, so overall, all the graphs will look like:

Notice that the expression can't have X be equal to 0 nor 3, that's because if they are either one of them, the denominator will be equal to zero, so in the end, the only integers that solve this inequality are: -3, -2, -1, 1 and 2.

-3-2-1+1+2 = -3.