Infinite Atwood Machine
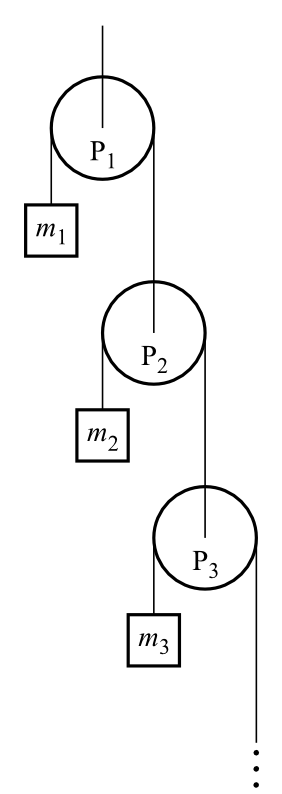 Consider the infinite Atwood’s machine shown below. A string passes over each
pulley, with one end attached to a mass and the other end attached to another
pulley. All the masses are equal to m, and all the pulleys and strings are massless.
The masses are held fixed and then simultaneously released. What is the acceleration
of the top mass?
Consider the infinite Atwood’s machine shown below. A string passes over each
pulley, with one end attached to a mass and the other end attached to another
pulley. All the masses are equal to m, and all the pulleys and strings are massless.
The masses are held fixed and then simultaneously released. What is the acceleration
of the top mass?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let the acceleration of top most particle is a as seen by topmost pulley. Then it will be in form as a=C g where C is any constant. If we change gravity by some factor keeping arrangement of system unchanged we will be find that acceleration will be replaced by same factor. This factor along with g is known as g(effective). Hence a=Cg(effective)
Now if we observe top most particle from top most pulley(since top most pulley is in rest g(effective) will be equal to g).
Then we can write..... a=Cg................(1)
Now if we observe the second topmost particle from frame of the second pulley then due to infinite pulley system second particle has same acceleration a as top most pulley but effective acceleration will be g-a then
We can write .... a=C(g-a)..............(2)
From equation (1) and (2)........................a=g/2=5................ANS
a=c(g-a) ; Cg=cg-ca; 0=ca Am I wrong? Which step
I solved this after reading this pdf ,might be a little bit difficult to understand, but the concept is absolutely correct!https://www.physics.harvard.edu/uploads/files/undergrad/probweek/sol43.pdf
I think you should have mentioned that g is 10m/s^2...... no offense intended....nice question!!!
if anybody could explain me how this answer came??
please explain ??????
Let the tension in the string above the first pulley be T. Then the tension in the string above the second pulley is T /2 (because the pulley is massless). Let the downward acceleration of the second pulley be a2. Then the second pulley effectively lives in a world where gravity has strength g − a2. Consider the subsystem of all the pulleys except the top one. This infinitesubsystem is identical to the original infinite system of all the pulleys. Therefore,by the arguments in the first paragraph above, we must have
\frac{T}{g} = \frac{\frac{T}{2}}{g- {a {2}}} ....... (1)
which gives a2 = g/2. But a2 is also the acceleration of the top mass, so our answeris g/2.
Remarks: You can show that the relative acceleration of the second and third pulleys is g/4, and that of the third and fourth is g/8, etc. The acceleration of a mass far down in the system therefore equals g(1/2 + 1/4 + 1/8 + · · ·) = g, which makes intuitive sense. Note that T = 0 also makes eq. (1) true. But this corresponds to putting a mass of zero at the end of a finite pulley system
Dont post copied solutions!
Why should g T = g − a 2 2 T ?
Instead shouldnt it be that m a 2 = T − m g m a 2 = 2 T − m ( g − a 2 )
(The downward acceleration of third pulley will also be a 2 )
∴ 2 T + − m ( g − a 2 ) T − m g = 1 and T = 2 m g
Whats wrong??
P.S Pls enclose your latex within \text{\[... }\) or [\text{ . . . }]
So this is the approach that I tried. If you consider the system attached to the right of the first pulley, it is another infinite Atwood machine - identical to the net system. If the tension in the string wrapped on the first pulley is T, the tension in the string to which the pulley is hooked is 2T (the pulley is massless). The system attached to the right of the pulley thus exerts this same 2T on the string (it's identical to the net system in the limit). Replace the system with a weight equal to 2T, that is of a mass of 2T/g. Now solve a two-body Atwood machine: T = m 1 + m 2 2 m 1 m 2 g ⟹ T = m + g 2 T 2 m g 2 T g ⟹ T = 2 3 m g . Hence, m a = 2 3 m g − m g = 2 m g ⟹ a = 2 g = 5 m s − 2 , given that g = 1 0 m s − 2 ( a is assumed upwards).