Infinite Atwood System
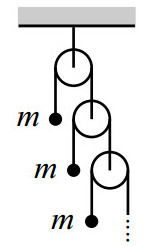 Consider a system of
infinite
pulleys as shown in the figure. Find the acceleration (in
) of the top mass.
Consider a system of
infinite
pulleys as shown in the figure. Find the acceleration (in
) of the top mass.
Details and Assumptions:
Initially the masses are held stationary, and then released simultaneously.
The masses of the pulleys and the strings are negligible.
The answer is 4.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the tension in the first string be T. Then, the tension in the second pulley string is T/2 as it is massless .Let the acceleration (downward) of the second pulley be a .Then the second pulley has the acceleration (g-a) .Now, suppose the other system expect the first one . This infinite system is identical to the previous system.Therefore, T / g = ( T / 2 ) / ( g − a ) which gives a = g / 2 = 9 . 8 / 2 = 4 . 9 m / s 2