Infinite Capacitor Oscillator
The LM555 is an integrated circuit that can accept analog signal to drive digital circuits.
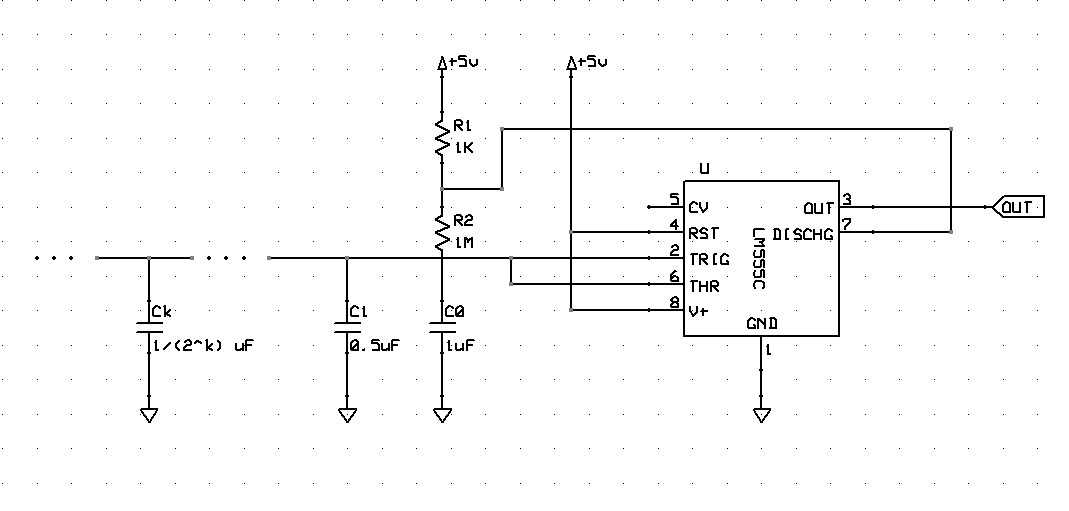
Assuming V c c = + 5 V and G N D = 0 V
It works as follows:
When pin 2 receives an input less than 3 1 of its V c c , pin 3 will give an output of + 5 V .
When pin 6 receives an input greater than 3 2 of its V c c , pin 3 will give an output of 0 V .
When pin 3 is 0 V , pin 7 is 0 V .
When pin 3 is 5 V , pin 7 has high impedance.
In the shown circuit, the LM 555 is configured as a clock circuit.
Calculate the period of OUT in seconds to the nearest hundreths.
The answer is 2.77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Phew, that took a while... I'm sure that this method can also be used to derive general formulas for the 555 Astable.
The circuit of the problem corresponds to the astable configuration of the LM555. As explained in the pages 10 and 11 of this PDF, the frecuency of oscillation is: f = ( R A + 2 R B ) C 1 . 4 4 And the period is: T = f 1 = 1 . 4 4 ( R A + 2 R B ) C Where R A is the resistance between pins 7 and 8 , R B is the resistance between pins 7 and 6 , and C is the capacitance between pin 6 and ground. Therefore: R A = 1 k Ω = 1 0 3 Ω R B = 1 M Ω = 1 0 6 Ω C = k = 0 ∑ ∞ 2 k 1 μ F = 2 μ F = 2 ⋅ 1 0 − 6 F Replacing: T = 1 . 4 4 ( 1 0 3 + 2 ⋅ 1 0 6 ) × 2 ⋅ 1 0 − 6 Ω F = 2 4 0 6 6 7 ≈ 2 . 7 7 9
First, we can compute the total capacitance C of the parallel capacitor array which, by observation, is given by the infinite sum: k = 0 ∑ ∞ ( 2 k 1 ) μ F
Therefore, by the infinite series formula: C = 2 μ F
Next, we look at the states of the circuit which determine the period of O U T .
Let the node of intersection of pin 2, pin 6, and the capacitor array be denoted as α . From the operation of the circuit, O U T is at V c c when V α ≤ 3 1 V c c . At this state, pin 7 has high impedance and the capacitor array can charge through resistors R 1 and R 2 , which have a total resistance of: R 1 + R 2 = 1 K Ω + 1 M Ω R 1 + R 2 = 1 , 0 0 1 , 0 0 0 Ω
After some t p seconds, V α reaches 3 2 V c c , changing the state of O U T to 0 V which also causes pin 7 to change to 0 V . The capacitor array then discharges through R 2 until V α reaches 3 1 V c c after some t n seconds, where the cycle repeats.
Let us assume, without loss of generality, that the period of O U T begins when O U T is at V c c , pin 7 has high impedance, and V α = 3 1 V c c .
The capacitor array V α charges through resistors R 1 and R 2 with an initial voltage E p which is defined as the input voltage with respect to the voltage of the capacitor: E p = V c c − 3 1 V c c = 3 2 V c c
The O U T = V c c half of the period ends when the capacitor voltage V α becomes 3 2 V c c after increasing by: Δ v p = 3 2 V c c − 3 1 V c c = 3 1 V c c
We can compute the time t p taken to charge the capacitor array to 3 2 V c c by using the formula for capacitor charge rate: t = R C ln ( 1 − E Δ v 1 )
t p = ( 1 , 0 0 1 , 0 0 0 Ω ) ( 2 μ F ) ln ⎝ ⎛ 1 − 3 2 V c c 3 1 V c c 1 ⎠ ⎞
t p = 1 . 3 8 7 6 8 0 6 5 5 s e c .
Now, O U T will become 0 V and V α will begin to discharge to 3 1 V c c (as previously mentioned) with a voltage E n . At this point, the voltage of the capacitor is 3 2 V c c and the input voltage to the capacitor is 0 V due to pin 7, so E n is: E n = 0 V − 3 2 V c c = − 3 2 V c c
To reach 3 1 V c c , the voltage V α must change by: Δ v n = 3 1 V c c − 3 2 V c c = − 3 1 V c c
The capacitor now only discharges through R 2 = 1 M Ω . We compute for the time of t n in a similar way to t p . t n = ( 1 M Ω ) ( 2 μ F ) ln ⎝ ⎛ 1 − − 3 2 V c c − 3 1 V c c 1 ⎠ ⎞
t n = 1 . 3 8 6 2 9 4 3 6 1 s e c .
Therefore, the period is: t p + t n = 1 . 3 8 7 6 8 0 6 5 5 + 1 . 3 8 6 2 9 4 3 6 1 s e c . t p + t n ≈ 2 . 7 7 s e c .