Infinite cuts and joints in Infinite disks
Initially there is a big disk of radius 10 in red then consecutively there is yellow disk cut out but with half the radius, then another red disk is added with as the radius similarly the process continue all the red disk have same mass density. Find the distance between the centre of the circle (radius = 10) and the centre of mass of the whole setup
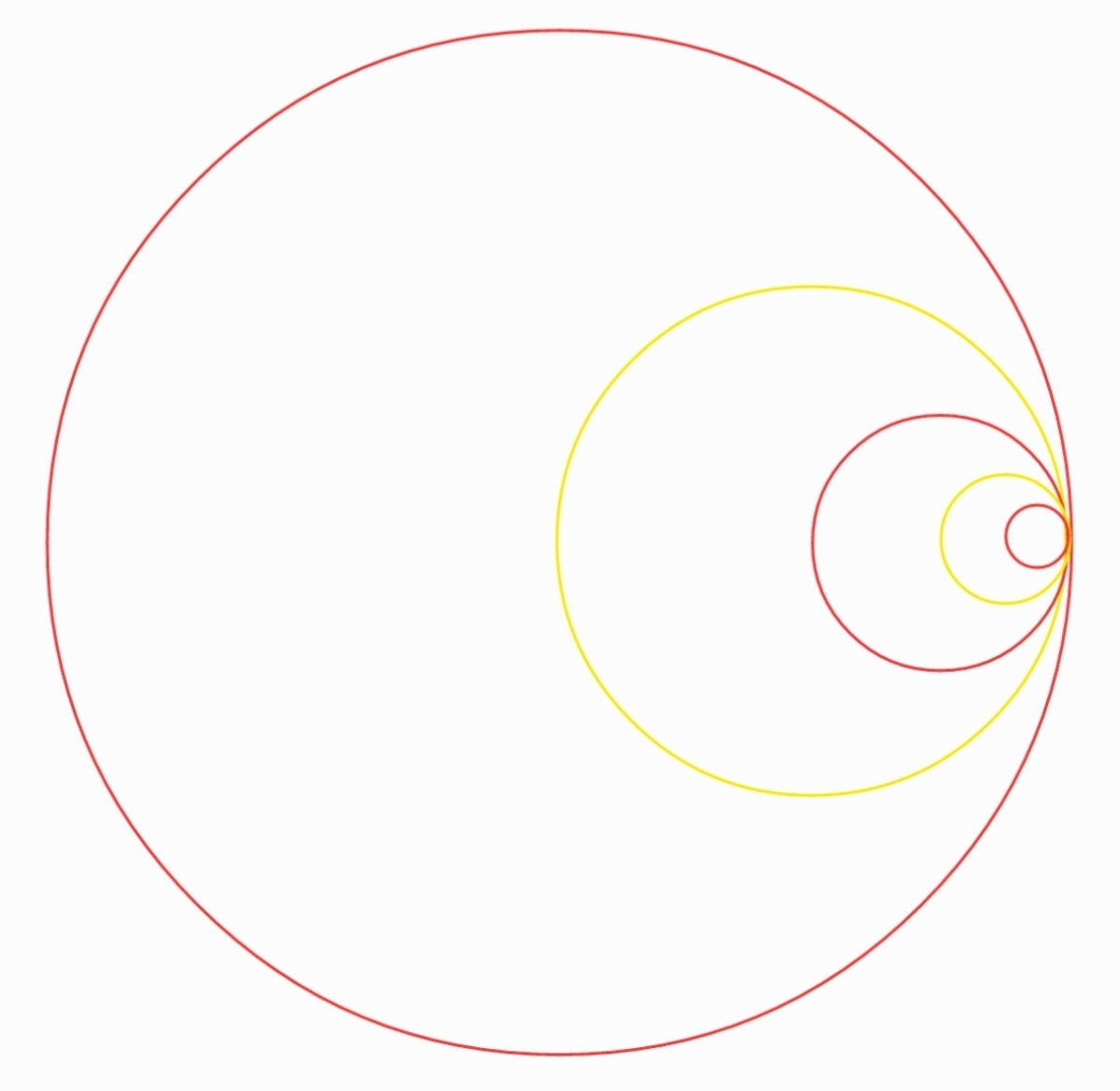 There are infinite circles in the picture
There are infinite circles in the picture
The answer is 1.1111111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the mass per unit area be m . The mass and location of X coordinate of the COM of the largest circle is:
M 0 = m ( π R 2 ) ; x 0 = 0 R = 1 0
Similarly, the mass and location of the X coordinate of the COM of the second-largest circle is:
M 1 = m ( 2 2 π R 2 ) ; x 1 = R − 2 R
That of the third-largest circle:
M 2 = m ( 4 2 π R 2 ) ; x 2 = R − 4 R
And so on. Generally, for the n-th largest circle:
M n = m ( 2 2 n π R 2 ) ; x n − 1 = R − 2 n R
The odd subscripts correspond to the yellow disks that are cut out and the even subscripts correspond to the red disks added. The X coordinate of the COM of this entire system is, therefore:
X C O M = M 0 − M 1 + M 2 − M 3 + M 4 … M 0 x 0 − M 1 x 1 + M 2 x 2 − M 3 x 3 + M 4 x 4 − M 5 x 5 + M 6 x 6 − … = D N
Where N and D can be generally written as: N = k = 0 ∑ ∞ ( − 1 ) k M k x k D = k = 0 ∑ ∞ ( − 1 ) k M k
⟹ N = k = 0 ∑ ∞ ( − 1 ) k m ( 2 2 k π R 2 ) ( R − 2 k R ) ⟹ D = k = 0 ∑ ∞ ( − 1 ) k m ( 2 2 k π R 2 )
I am leaving out the steps of the final calculations. The answer is X C O M ≈ − 1 . 1 1 1 . Since the location of the COM of the largest full circle is the origin, the required answer is ≈ 1 . 1 1 1