Infinite dimensions, not quite infinite volume
The real number satisfies the equation above and can be expressed in the form , with and positive, root-free integers with a greatest common divisor of 2. Find .
If you believe that the following limit goes to infinity for all real , submit your answer as 2016.
Details and Assumptions
denotes Euler's number, the base of the natural logarithm.
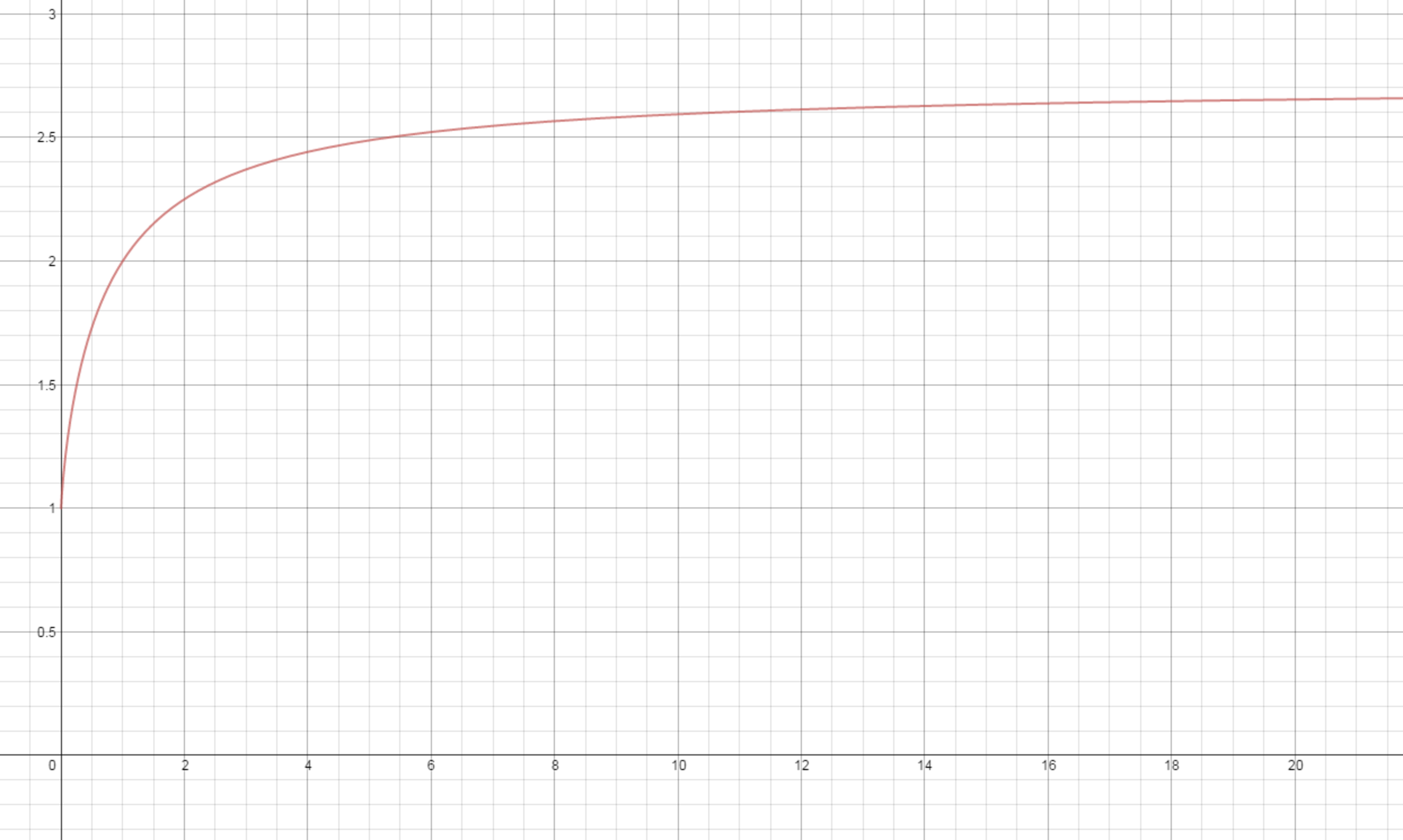
This problem is original. The picture of the graph was produced from Desmos .
The answer is 46.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we evaluate the integral using the substitution u = x + y 2 : \left(1+6\int_{0}^B \frac{y\left(x+y^2\right)^2}{x^3}dy\right)^x= \left(1+\frac{\left(x+y^2\right)^3}{x^3}\bigg{|}_0^B\right)^x= \left(1+\frac{\left(x+B^2\right)^3}{x^3}-1\right)^x=\left(\frac{\left(x+B^2\right)}{x}\right)^{3x}
This is an indeterminate form of the type 1 ∞ , so we will convert to to exp ( ln ( x ( x + B 2 ) ) 3 x ) = exp ( 3 x ln ( x ( x + B 2 ) ) ) = exp ( 3 x ( ln ( x + B 2 ) − ln x ) )
The equation inside the exp is now an indeterminate form of the type 0 ⋅ ∞ , so we will modify it to be exp ( 3 x 1 ln ( x + B 2 ) − ln x ) then apply L'Hospital's Rule:
exp ( 3 x 1 ln ( x + B 2 ) − ln x ) = ( − 3 x 2 1 x + B 2 1 − x 1 ) = exp ( − x + B 2 3 x 2 + 3 x )
Long dividing the first term, we get
− 3 x + 3 B 2 − x + B 2 3 B 4 + 3 x = 3 B 2 − x + B 2 3 B 4
Finally, because x is going to ∞ , we obtain the limit as e 3 B 2
We are looking for the term in the exponent to be 2016.
3 B 2 = 2 0 1 6
B 2 = 6 7 2
B = 6 7 2 = 4 4 2
α = 4 , β = 4 2 , α + β = 4 6