Infinite Geometrical Geometric Series!
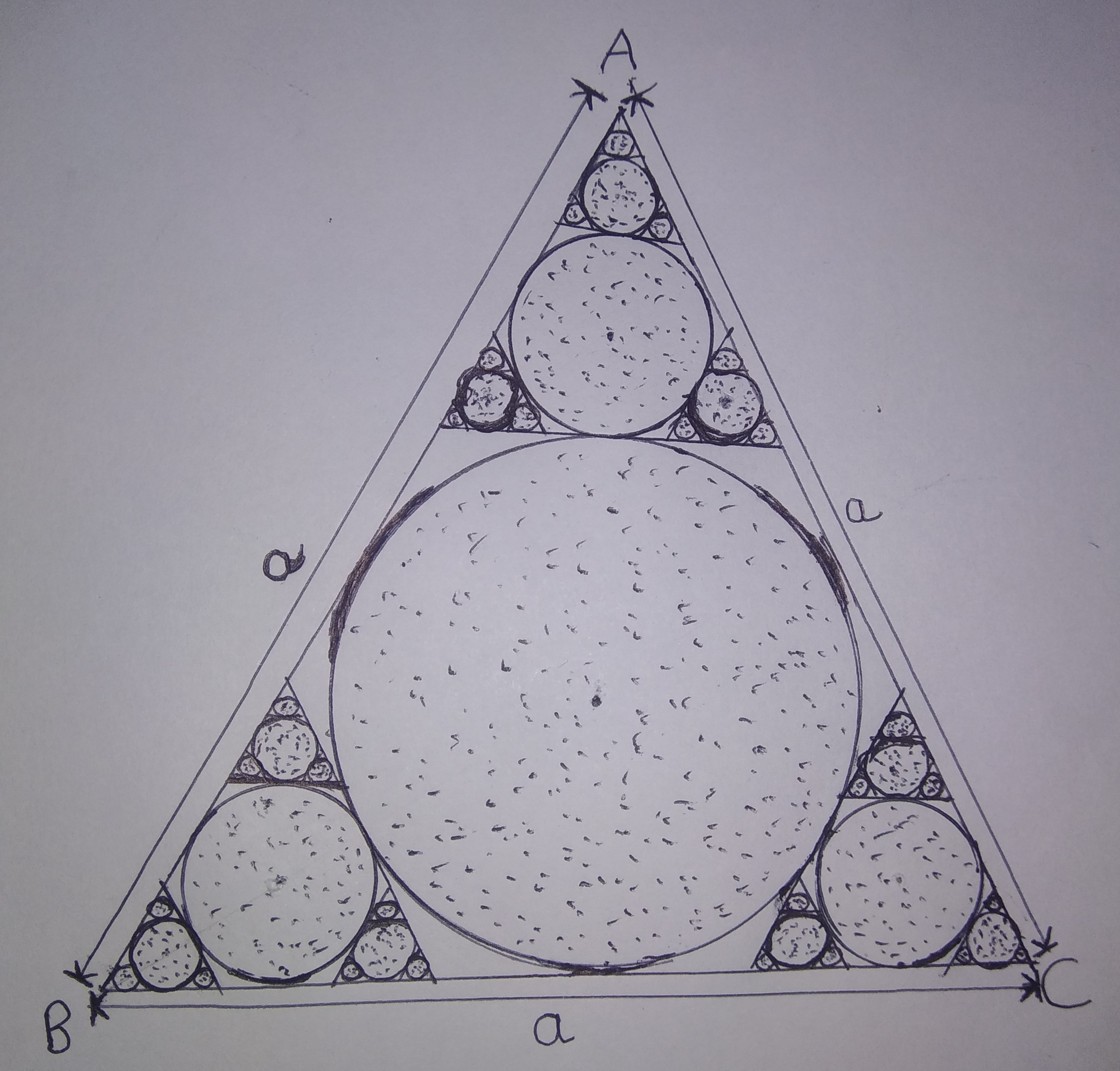
Above figure consists of ∞ circles inscribed in an Equilateral Triangle in a pattern as shown above. Let Area of Infinite circles = A 1 ( dotted region ) and Area of Equilateral Triangle Δ A B C = A 2 .
Find value of A 2 A 1 . If your answer is of form x π , enter answer as x .
All of my problems are original
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice problem and a nice solution.
I just calculated the ratio between the largest circle and the largest inner hexagon, the pattern is repeated, my answer was 12 too.
Log in to reply
Ohk, that's nice. Do share your solution with us. :)
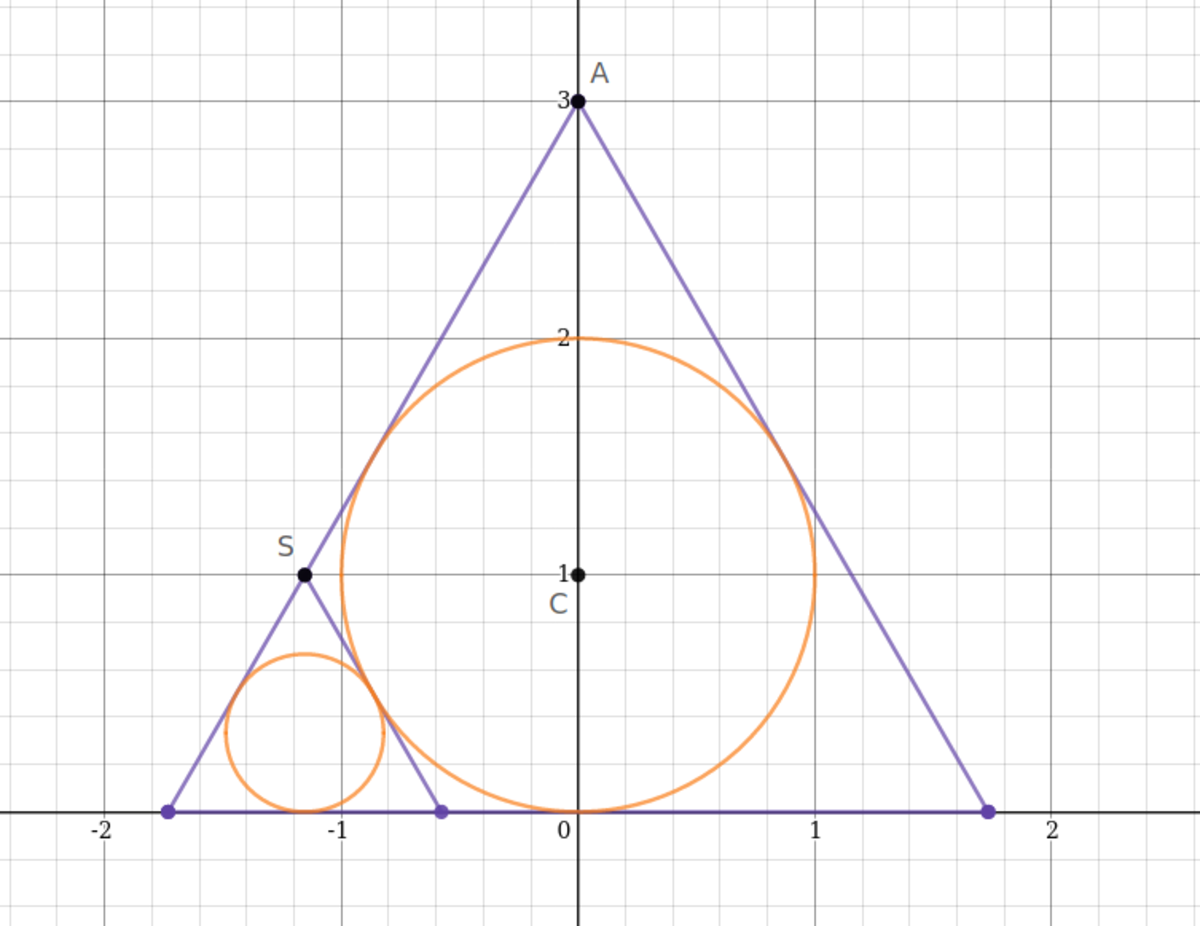 The smaller triangle is just a scaled version of the bigger one.
The smaller triangle is just a scaled version of the bigger one.
Let the ratio of the area of all the circles inside a triangle to the area of the triangle be y . Hence, y = A 2 A 1 . This is our desired quantity. Notice that y doesn't depend on the size of the triangle. This observation will be extremely useful.
Denote the area of the smaller triangle S by s . The area of all the circles inside it will be s y . (I have shown just one circle inside the smaller triangle, but there are infinitely many.)
There are 3 such smaller triangles (congruent to S ) inside the bigger one. (The other two aren't shown in the above diagram.)
Now, let's focus on the bigger triangle A . Denote its area by a . The total area of all the circles inside A is then a y . Also, let the area of the circle C , which is inscribed in A , be c .
The area of all the circles inside A can be calculated as the sum of the area of the inscribed circle and the area of all the circles inside the 3 smaller triangles. So,
a y = c + 3 s y ⟹ y = a − 3 s c
Assume, C has a radius of r . The side length of A will then be 2 3 r . And the side length of S will be 3 2 3 r .
So, c = π r 2 , a = 3 3 r 2 , s = 9 3 3 r 2 .
y = 3 3 r 2 − 3 ( 9 3 3 r 2 ) π r 2 ∴ y = 2 3 π = 1 2 π
Excellent solution sir. Thanku for sharing it with us.
Nice solution SIR .
a very different but fresh approach really enjoyed it
Since the pattern is repeated, the ratio of area of the infinite circles to the area of whole triangle ABC will be equal to the ratio of area of the largest circle to the area of the largest hexagon .
Area of the large hexagon:
→ a r ∆ A B C − 3 × a r (other three small equilateral triangles with sides 3 a )
→ 4 √ 3 a ² − 3 × [ 4 √ 3 × 3 ² a ² ]
→ 6 √ 3 a ²
The radius of the circle inscribed in an equilateral triangle is given by
r = 6 √ 3 a
(You should derive it yourself), where a is the side of the triangle, here ∆ABC
Area of the largest circle:
→ π r ² = π × [ 6 √ 3 a ] ²
→ 3 6 3 π a ²
Ratio asked is small's to large's, so circle to hexagon:
→ 6 √ 3 a ² 3 6 3 π a ² = 6 √ 3 π = 6 √ 3 3 π = 2 √ 3 π = √ 1 2 π
So x=12
Excellent solution sir. Thanku for sharing it with us. :)
To have the same picture in mind, the height(or angle bisector or median) I'm talking about is the one from vertex A to BC(call the intersection D). the n th circles are labeled C n
In an equilateral triangle, the angle bisector, median, and the height are the same line; the center of the inscribed circle is the intersection of the angle bisectors(which in this case are also the medians); the medians cut each other to have a 1:2 ratio(the distance between the center and the side is 3 1 the median and the one between the center and vertex is 3 2 the median) so the distance between the circle's center and the side(which is the radius) is 3 1 the height(which is also the median) making 3 2 the height the diameter of the circle so the height of the smaller triangle(which is the part of the median minus the diameter[which is perpendicular since the base of ABC and the base of the smaller triangle are parallel by corresponding angles]) is 3 1 the height.
In other words, the ratio between the height of the big triangle ABC to the height of the second largest triangle is 3 1 so it follows that the ratio the areas of the circles inscribed in the big triangle to the 2nd biggest is 9 1 (it follows either by similarity or by simply doing the same process to get the new radius and find that π ( 3 r ) 2 π r 2 = 9 1 ).
The sum of the circles' areas are C 1 + 3 C 2 + 3 2 C 3 + 3 3 C 4 + 3 4 C 4 + ⋯ and each circle is 9 1 the area of the other so let that sum is C 1 + 3 ( 9 1 C 1 ) + 3 2 ( 9 2 1 C 1 ) + 3 3 ( 9 3 1 C 1 ) + 3 4 ( 9 4 1 C 1 ) + ⋅ = C 1 ( 1 + 3 1 + 3 2 1 + 3 3 1 + 3 4 1 + ⋯ ) = 2 3 C 1 .
If the height of ABC hits BC at D then triangle ABD is a 30-60-90 triangle so the height is 2 a 3 . Since the radius of C 1 is 3 1 the height, the radius of C 1 is 6 a 3 . Therefore, the sum of all circles' areas is 2 3 C 1 = 2 3 π ( 6 a 3 ) 2 = 8 a 2 / p i = A 1
The area of ABC is simply half the base times the height: 2 1 ( a ) ( 2 a 3 = 4 a 2 3 = A 2
Therefore A 2 A 1 = 4 a 2 3 8 a 2 / p i = 2 3 π = 1 2 π
So x = 1 2 .
Excellent solution sir. Thanku for sharing it with us. :)
Let us number each circle as per their nested degree.
Now, you could prove yourself,
Radius of n t h circle = r n = 3 r n − 1
r n = 3 1 r n − 1 = 3 2 r n − 2 = … = 3 n − 1 r 1
Now,
Area of n t h nest = A n = Number of circles × π r n 2
A n = 3 n − 1 × π ( 3 n − 1 r 1 ) 2 = π 3 n − 1 r 1 2
Total area = n = 1 ∑ ∞ A n
Total area = n = 1 ∑ ∞ π 3 n − 1 r 1 2
Total area = π 2 3 r 1 2
Total area = π 2 3 ( 2 3 a ) 2
Total area = π 8 a 2
r a t i o = 4 3 a 2 π 8 a 2
r a t i o = 1 2 π
Visualisation: dotted region is about 9 0 . 6 8 % of the triangle's area