Infinite Geometric Progression
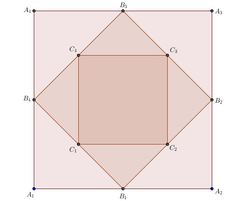 A square
B
1
B
2
B
3
B
4
is formed by joining the midpoints of the sides of a square
A
1
A
2
A
3
A
4
. A third square
C
1
C
2
C
3
C
4
is made in the same way and the process is continued indefinitely.
A square
B
1
B
2
B
3
B
4
is formed by joining the midpoints of the sides of a square
A
1
A
2
A
3
A
4
. A third square
C
1
C
2
C
3
C
4
is made in the same way and the process is continued indefinitely.
If A 1 A 2 = 1 0 cm , find the sum of the areas of all the squares so formed in cm 2 .
The answer is 200.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ok! But I can't edit it now!
Hey! @Ameya Salankar - I've already posted a solution? Why d'ya need to post another?
Log in to reply
@Krishna Ar , When you posted your solution, I was writing the last line of MY solution. And when I clicked on Publish , then only I saw your solution. But, what's the problem with that?
Yaa you should
Let S be the required sum.
B 1 B 2 = ( A 2 B 1 ) 2 + ( A 2 B 2 ) 2 = 5 2 + 5 2 = 5 2 c m .
Similarly,
C
1
C
2
=
5
c
m
&
the side of the fourth such square is
2
5
c
m
.
Therefore, the sum of the areas of all the squares so formed is the sum of an infinite Geometric Progression with first term as 1 0 0 & common ratio as ( 2 1 ) 2 = 2 1 .
Sum of an infinite G.P. =
1
−
r
a
where
a
is the first term &
r
is the common ratio.
(This formula works only when
∣
r
∣
<
1
. For
∣
r
∣
>
1
, the sum tends to infinity.)
⇒ S = 1 − 2 1 1 0 0 = 2 0 0 c m 2 .
The question is quite clear in itself! It is an infinite G.P with Initial term = 100 and common ratio=0.5 THis we can see quite clearly from the facts that the areas are 100 (10*10), 50 ( midpoints are joined to form a square, thus area is halved), and thus area is halved indefinitely.
WE know the formula for infinite G.P to be- 1 − r a . This is where A=100 and R=0.5 . Applying this we get 100/0.5= 200. Done!
@Ameya Salankar - you should not have titled the question as "Infinte G.p"