Infinite Inscription
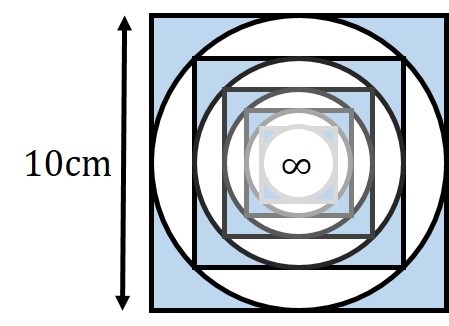 Start with a
1
0
cm
×
1
0
cm
square. Within this square, inscribe a circle, and shade the area between this circle and the original square blue. Within this circle, inscribe another square. Repeat the process an infinite number of times.
Start with a
1
0
cm
×
1
0
cm
square. Within this square, inscribe a circle, and shade the area between this circle and the original square blue. Within this circle, inscribe another square. Repeat the process an infinite number of times.
What is the area of the blue shaded region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There is a simpler way of doing this (I think):
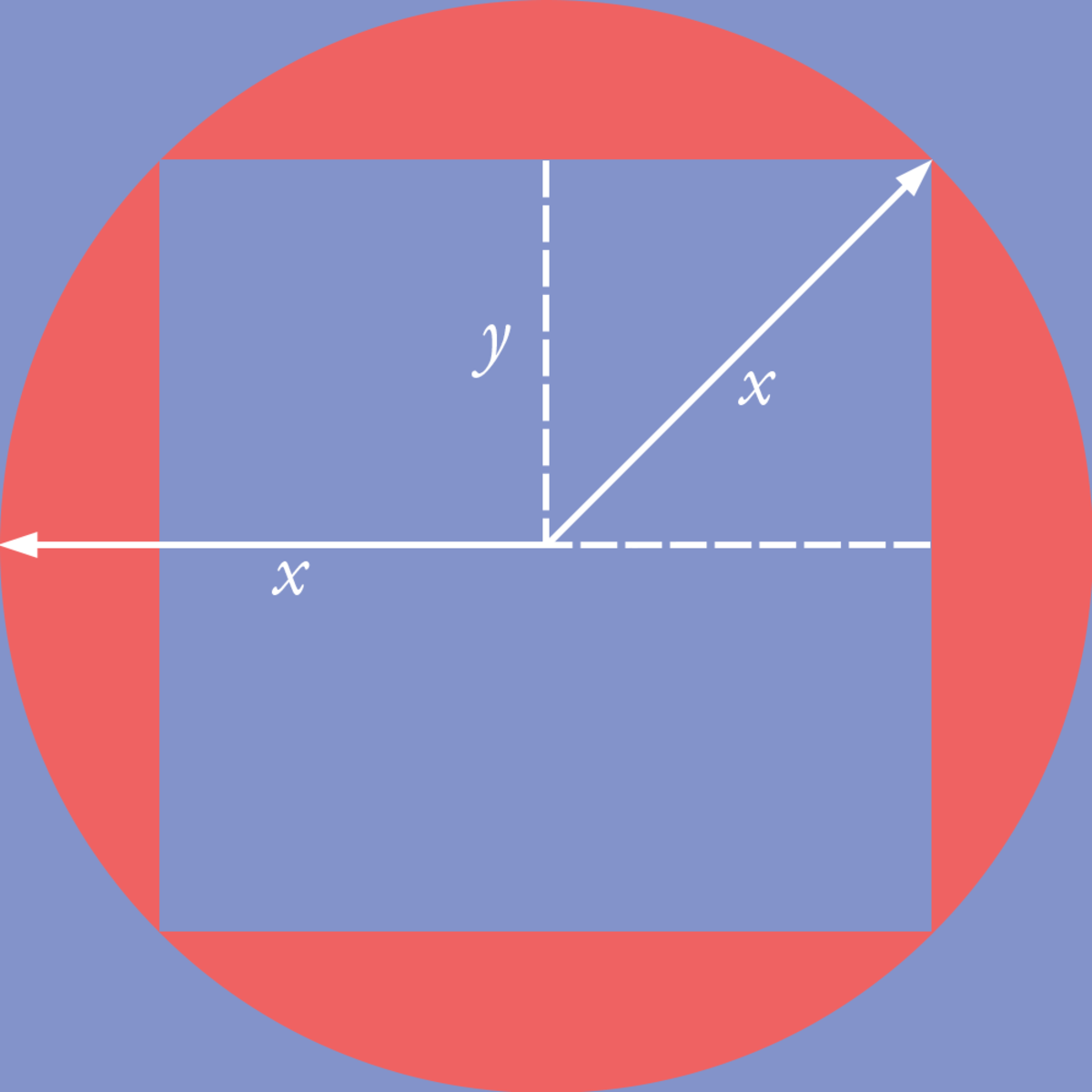
In this diagram, the area of the big square is ( 2 x ) 2 = 4 x 2 . Pythagoras tells us that x 2 = 2 ( y 2 ) , so x = 2 y and y = 2 x . Therefore, the area of the small square is ( 2 y ) 2 = ( 2 x ) 2 = 2 x 2 . Thus, the area of the small square is half that of the large one. The ratio of sum of the areas of all the squares to the area of the first square is ∑ n = 0 ∞ 2 n 1 = 2 . We simply multiply the area of the first blue shaded region by 2, which gives 2 ∗ ( 1 0 0 − 2 5 π ) = 2 0 0 − 5 0 π . ■
We can find the answer to this question by removing the options.
The answer has to be less than 100 so option 1 removed.
Option 2 is negative therefore removed.
Option 4 is not possible.
Thus, option 3 is the answer.
It might help to work out the area of the first few squares and circles.
The area of the first square is clearly 1 0 0 cm 2 . Meanwhile, the first circle's radius is equal to half the first square's side length, so its area is π × 5 2 = 2 5 π . So the area of the first shaded region is 1 0 0 − 2 5 π .
Using Pythagoras' Theorem yields the side length of the second square. x 2 = 5 2 + 5 2 = 5 0 so x = 5 0 . This yields that the area of the second square is 5 0 2 = 5 0 . It also yields that the radius of the second circle is ( 2 5 0 ) 2 , so the area of the second circle is π × ( 2 5 0 ) 2 = 1 2 . 2 5 π . So the area of the second blue region is 5 0 − 1 2 . 2 5 π .
You can repeat these calculations for the next few squares and circles if you like, but the pattern is already quite clear; the total area of the blue region will be given by:
( 1 0 0 − 2 5 π ) + ( 5 0 − 1 2 . 2 5 π ) + ( 2 5 − 6 . 2 5 π + ) . . .
Rearranging yields a slightly clearer format:
( 1 0 0 + 5 0 + 2 5 + . . . ) − π ( 2 5 + 1 2 . 5 + 6 . 2 5 + . . . ) .
These are two geometric series whose sums to infinity can be calculated using S ∞ = 1 − r a . Hence, the sum of the first series is 1 − 2 1 1 0 0 = 2 0 0 and the sum of the second series is 1 − 2 1 2 5 = 5 0 .
So the blue area is 2 0 0 − 5 0 π .
QED.