Infinite L'Hôpital's Rule!

$\displaystyle\lim_{x\rightarrow0}\dfrac{\cot(x)}{\csc(x)}=\displaystyle\lim_{x\rightarrow0}\dfrac{\frac{\cos(x)}{\sin(x)}}{\frac{1}{\sin(x)}}=\displaystyle\lim_{x\rightarrow0}\dfrac{\cos(x)}{1}=\cos(0)=\boxed{1}$

If one insists on using L'Hôpital's Rule,

Let $\text{L}= \lim\limits_{x \to 0} \frac{\cot(x)}{\csc(x)} = \lim\limits_{x \to 0}\frac{\csc(x)}{\cot(x)}$ (using L' Hospital Rule)

$\implies \text{L}=\dfrac{1}{\text{L}}$

$\implies \text{L}= \pm 1$
$\implies \boxed{\text{L}=1}$ $\left( \ -1 \ \text{is rejected since the ratio} \ \ \dfrac{\cot(x)}{\csc(x)} \ \ \text{is positive near} \ \ 0 \ \ \right)$

$\lim _{ x\rightarrow 0 }{ \frac { \cot { x } }{ \csc { x } } } \\ =\lim _{ x\rightarrow 0 }{ \frac { \frac { \cos { x } }{ \sin { x } } }{ \frac { 1 }{ \sin { x } } } } \\ =\lim _{ x\rightarrow 0 }{ \cos { x } } \\ =1$

No need to apply L-Hospital's. Simplify the expression by converting into sine and cosine to get $lim_{x→0}cosx$ to get answer 1

I put absolutley no thought into this and just typed 1 and it was correct

$\lim _{ x\rightarrow 0 }{ \frac { \cot { (x) } }{ \csc { (x) } } } =\quad \lim _{ x\rightarrow 0 }{ \frac { \cos { (x) } }{ \sin { (x) } } } \div \frac { 1 }{ \sin { (x) } } \quad =\quad \lim _{ x\rightarrow 0 }{ \cos { (x) } } =\quad \cos { (0)\quad } =\quad 1$

also done the same

ha ha ha very funny ..:) "Please help me! I kept using L'Hôpital's rule millions of times and I can't evaluate the limit!" love your humor.. cot x / cosec x = cosx...lim x>0 cos x = 1

just simplify the trig ratio to be cos(x) , then the value of cos(0) is 1

Why are you keep on doing the lazy solution. this is actually the solution. lol hahaha

cot(x) = cos(x)/sin(x) csc(x) = sin (x)

cot(x)/csc(x) = cos(x)

limit as x->0 is 1. lol

I think you do not need to use L'Hopital rule

You just evaluate by manipulating it: limit(((cot(x))/(csc(x)))= limit(((((cos(x))/(sin(x))))/(((1)/(sin(x)))))= limit(((cos(x))/(sin(x)))·sin(x)= limit(cos(x)=1,x,0),x,0),x,0),x,0)

cot(x)/csc(x) = sin(x)/tan(x) now use L' Hospital's rule

Cotx= cosx/sinx ; cosecx = 1/sinx ; thus cosx/cosecx=cosx as x-> 0 means x is not equal to 0 . Thus lim(x->0)cosx = 1

You can convert cot and cosec into sin and cos then only cos(x) will remain and cos (0) is 1

Multiply and divide the given limit with x. And then use the taylor expansion for x cot(x) and x cosec (x) and then substitute x=0 to get the answer, that is 1

If you wanted to solve the above limit problem by only using L'Hospital rule,You have to little bit manipulate the function as follows

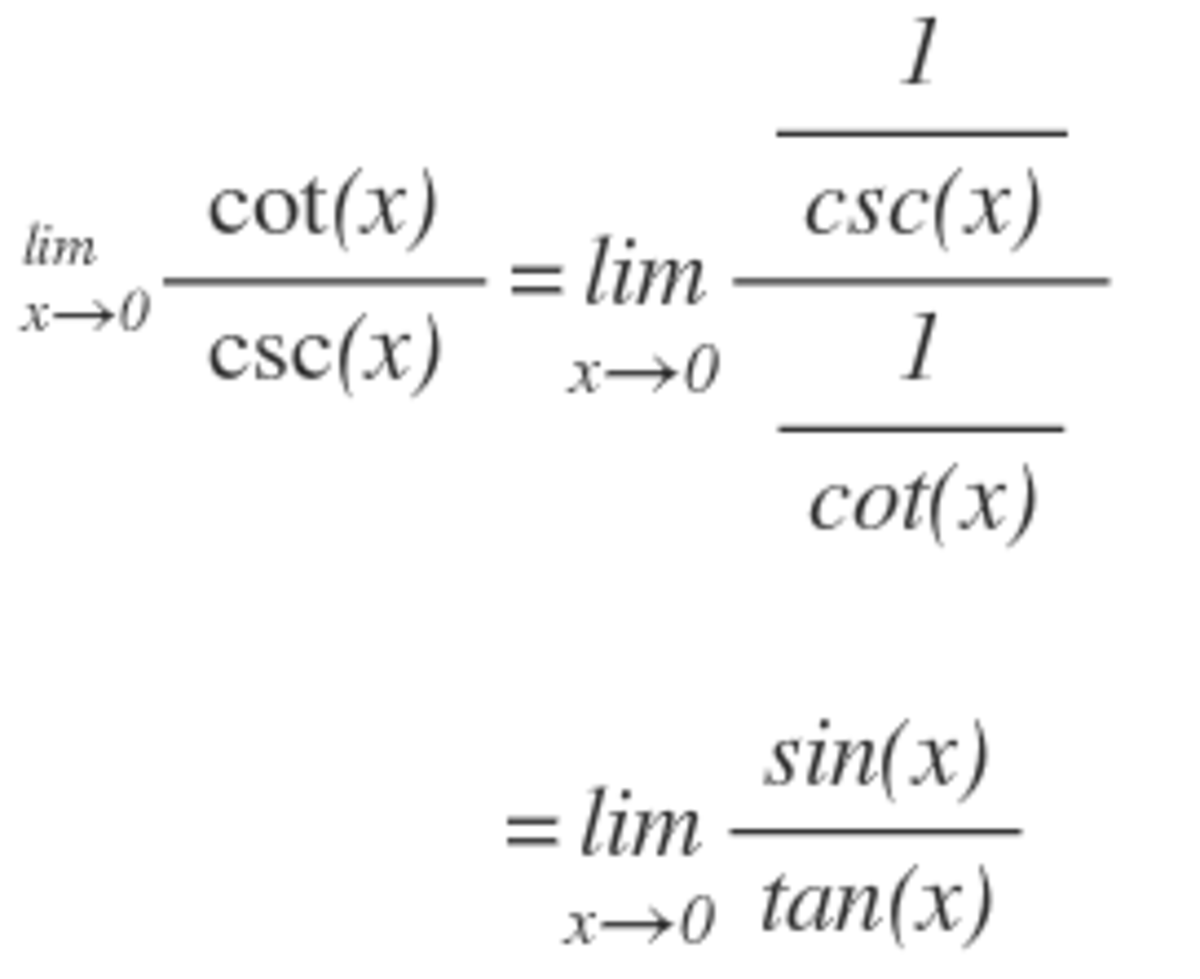Now apply L'Hospital rule