Infinite Nested Radical Product
Find p : (Report your answer to 5 places after decimal)
5 2 ⋅ 3 − ϕ 1 ⋅ s → ∞ lim 2 s 1 ⋅ k = 1 ∏ s ( Δ k ) = p 1
where, Δ m = m r o o t s 2 + 2 + 2 + ⋯ + 2 + 2 + ϕ
and, ϕ = 2 1 + 5 is the Golden Ratio.
For example: Δ 1 = 2 + ϕ , Δ 3 = 2 + 2 + 2 + ϕ , etc.
The answer is 3.14159.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The 2 equations you have written after "we know" is amazing. May you send proof for those Equation??
Log in to reply
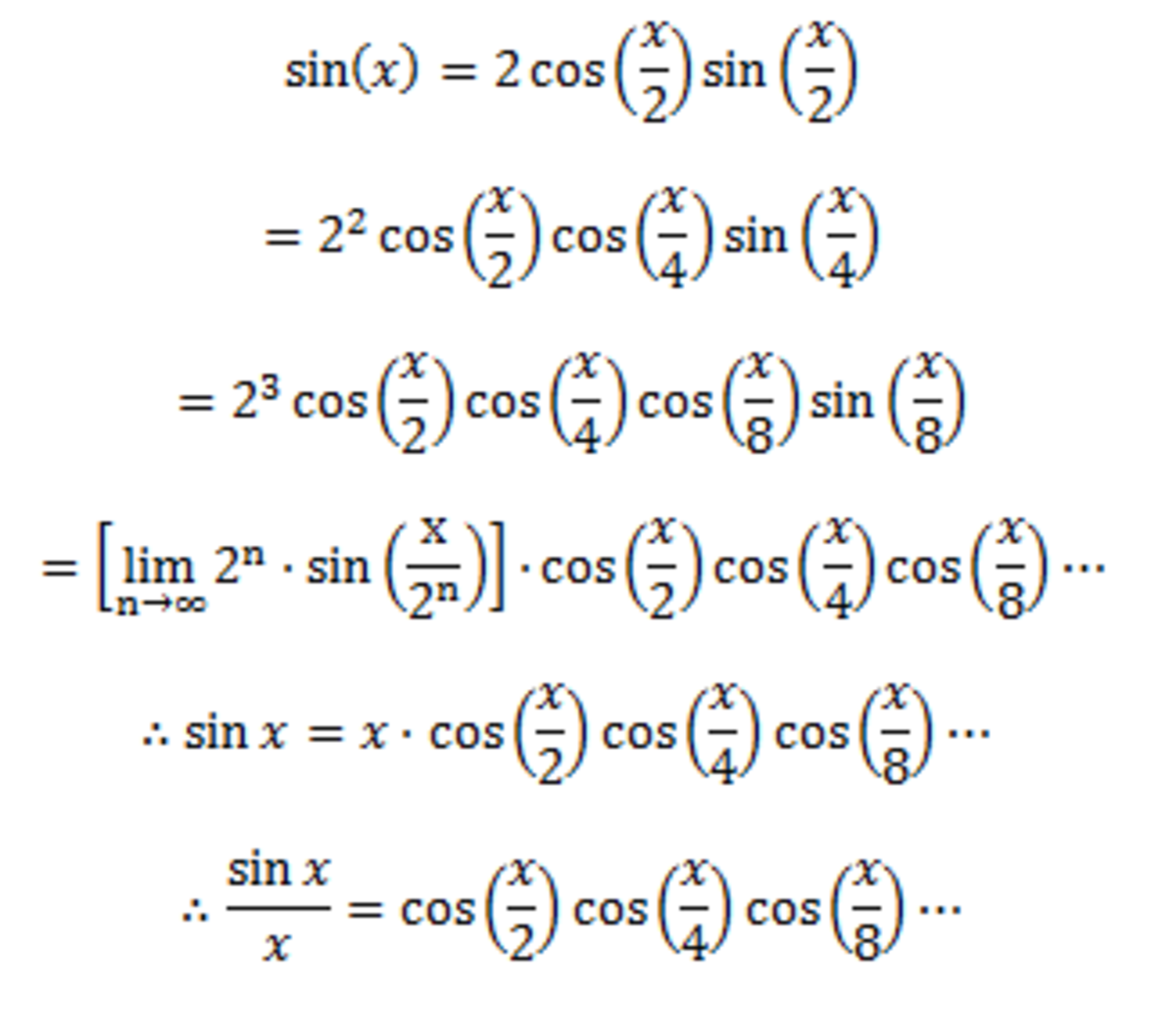
We know,
θ sin θ = cos 2 θ ⋅ cos 4 θ ⋅ cos 8 θ ⋅ cos 1 6 θ ⋅ cos 3 2 θ ⋯
Putting θ = 5 π we get:
2 ⋅ π 5 ⋅ 3 − ϕ = cos 1 0 π ⋅ cos 2 0 π ⋅ cos 4 0 π ⋅ cos 8 0 π ⋅ cos 1 6 0 π ⋯
Also we know, cos 1 0 n π = 2 1 Δ m = 2 1 m r o o t s 2 + 2 + 2 + ⋯ + 2 + 2 + ϕ
hence,
5 2 ⋅ 3 − ϕ 1 ⋅ s → ∞ lim 2 s 1 ⋅ k = 0 ∏ s ( Δ 2 k ) = π 1 ∴ p = π ≈ 3 . 1 4 1 5 9