Infinite RC Circuit-2!
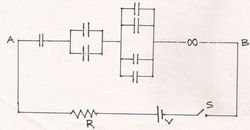 In the given network shown, each capacitor is of capacitance
. The switch is closed at
.
In the given network shown, each capacitor is of capacitance
. The switch is closed at
.
Which of these statements is/are true?
1) Time Constant for the Circuit is
.
2) Left most capacitor will have highest charge.
3) Capacitors will have increasingly high potential differences across them as we move toward the right.
4) Total heat generated in the circuit is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Capacitors in parallel add as: C P = C 1 + C 2 + . . . while capacitors in series add as: 1 / C S = 1 / C 1 + 1 / C 2 + . . .
So, we can easily turn the arrangement of capacitors into: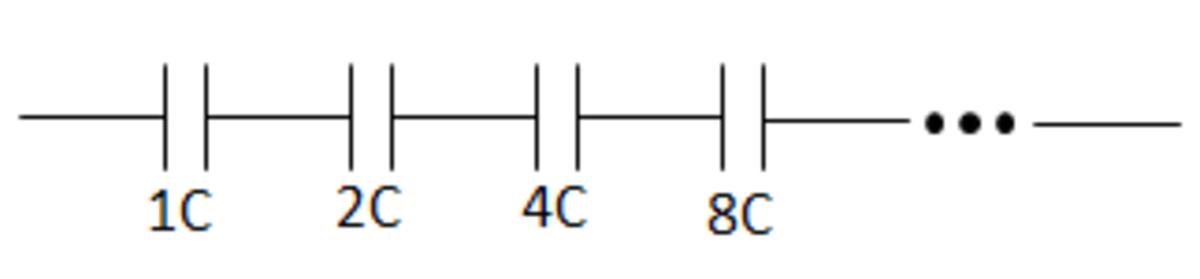
Now, when we combine these in series we get C T 1 = C 1 + 2 C 1 + 4 C 1 + 8 C 1 + . . . , the right side of which is just a geometric series with a sum of C 2 . Therefore, the total (or equivalent) capacitance is just C / 2 .
With the circuit simplified, we can now answer each of the questions:
1) For an R C circuit, τ = R C , so in this case, τ = R C / 2 . ⇒ TRUE
2) In series, all capacitors will hold an equal amount of charge. This means that in the circuit I showed above, each capacitor holds the same amount. BUT, since each capacitor was a parallel sum of other capacitors, each of these capacitors will hold only a fraction of that charge. So, as we move towards the right, the charge is split among more and more capacitors. Therefore, the leftmost capacitors holds the most. ⇒ TRUE
3) The potential difference across a capacitor with charge Q is given by V = Q / C . With equal amounts of charge, the potential difference is inversely proportional to the capacitance, so as we move to the right and have increasing capacitance, we will necessarily have decreasing potential difference. ⇒ FALSE
4) An ideal battery maintains a constant potential difference, V , where V = U / Q . So, when an amount of charge, Q , is "pushed" by the battery, it carries an energy equivalent of Q V . We can write this in terms of capacitance as C V 2 But, the energy stored by a capacitor is given by the familiar U = 2 1 C V 2 . Clearly, if the battery sources C V 2 but the capacitor only keeps U = 2 1 C V 2 , the remaining U = 2 1 C V 2 must be "lost" in the form of heat. Here, the capacitance is really C / 2 , so the amount lost to heat is U = 4 1 C V 2 . ⇒ FALSE