Infinite RC Circuit!
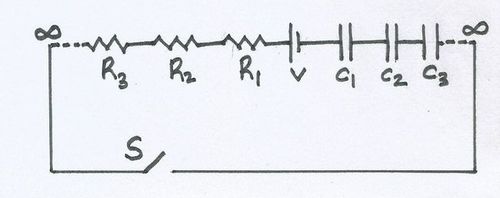 In the circuit shown, we have infinitely many resistors with resistance of
R
1
=
R
,
R
2
=
2
R
,
R
3
=
4
R
,
…
. We also have infinitely many capacitors with capacitance of
C
1
=
C
,
C
2
=
2
C
,
C
3
=
4
C
,
…
. At
t
=
0
switch S is closed.
In the circuit shown, we have infinitely many resistors with resistance of
R
1
=
R
,
R
2
=
2
R
,
R
3
=
4
R
,
…
. We also have infinitely many capacitors with capacitance of
C
1
=
C
,
C
2
=
2
C
,
C
3
=
4
C
,
…
. At
t
=
0
switch S is closed.
Find the ratio of potential drop (in volts) across capacitor C n and resistor R n at time t = R eq C eq . Take e = 2 . 7 1 8 .
The answer is 1.718.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It must be specified if its 1 time constant or just RC!!
Log in to reply
here one time constant and RC have the same values!
Req
= 2R using infinite G.P series.
Similarly,
Ceq
= C/2.
Now use formula.
for capacitor
Vc=V[1-e^(t/CR)]
for resistor which is
Vr=V[e^(t/CR)]
and as given t=CR
Now just take ratio and u'll get the answer
The equivalent series resistance is:
R e q = R + 2 R + 4 R + … = R ( 1 + 2 1 + 4 1 + … ) R e q = 2 R
The equivalent series capacitance is:
C e q = C 1 + 2 C 1 + 4 C 1 + … 1 = C 1 ( 1 + 2 1 + 4 1 + … ) 1 C e q = 2 C
The time constant of the equivalent RC circuit is:
τ = R e q C e q = R C
The equivalent capacitor voltage in a RC circuit at a given time t is V C = V ( 1 − e − t / τ ) and the equivalent resistor voltage is V R = V e − t / τ . Therefore, at a time t = R C :
V C = V ( 1 − e − 1 ) , V R = V e − 1
The quotient of voltages is:
V R V C = V e − 1 V ( 1 − e − 1 ) = e − 1 ≈ 1 . 7 1 8