Infinite Resistors

We should assume that there is a battery of emf V' connected between two points of a small square. Lets say the points are A and B. If current supplied by battery is I then from symmetry of the figure,current in all wires is same. This curretn equal to half of current supplied by the battery. V'=I'Req For circuit, V'=I'/2R' I'Req=I'/2R' so,Req=R'/2.

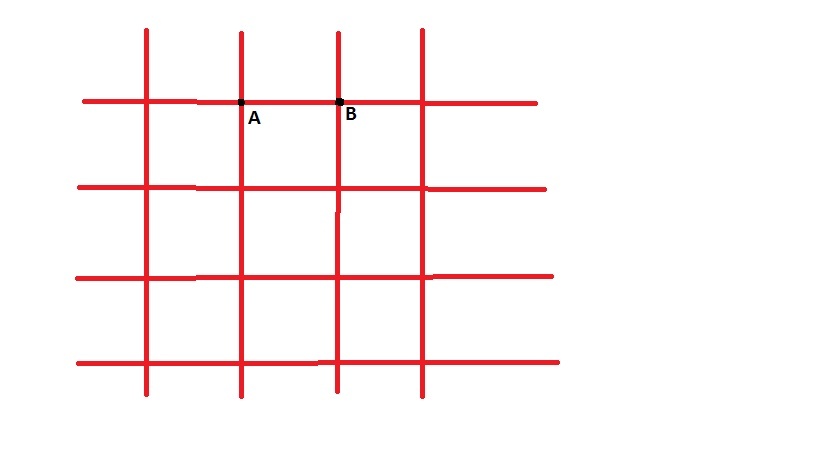Small part of the infinite grid of resistors

---

So let's do a thought experiment!

Imagine voltage $V$ be applied across the points $A$ and $B$ . If $I$ current flows into point $A$ , then it would divide into four equal parts by symmetry, and thus $AB$ would carry current $\frac{I}{4}$ . Similarly, $\frac{I}{4}$ currents flows in $AB$ , when $I$ current is injected to $B$ . Using Principle of Superposition, ${I}_{net} = \frac{I}{2}$ . As the entire part of the infinite grid is in parallel to $AB$ , we can conclude that the equivalent resistance is $\frac{R}{2} = 0.5 \Omega$ .