Infinite resistors+GP+Quadratics!!
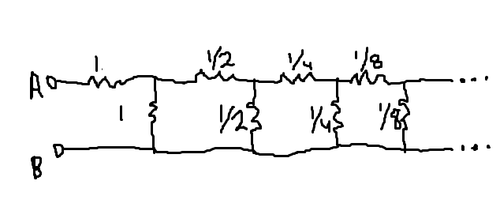Find the equivalent resistance through A and B. (All values in Ohms)
The answer is 1.414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
sol
How can we write that resistance between c&d is R/2? Pls explain.
Log in to reply
Good question, it is the only thing in this question which requires a good analyzing power. See carefully that all the combination of resistance across A and B we say that their equivalent would be R than here we can see that : R = one 1ohm resistance in series then one in parallel then half in series then half in parallel and then 1/4 in series and in parallel and it goes on. So you can see that across C and D there is one 1/2ohm resis. in series then 1/2 in parallel then 1/4 in series and parallel and then 1/8 in series and parallel and goes to infinity. So all the combination of resistances which make up R are now halved across C and D so we can conclude that here equivalent resistance will be R/2.
if we add 2ohm resistance behind 1ohm in such a way that a G.P continues but starts from 2 ...in that case this method wouldn't work ....
Denote the overall resistance as R . For convenience, we will refer to the first intersection of A's row as A 1 . Observe that the resistance between A 1 and B is equivalent to 1 + 2 R 1 1 , by the formula for parallel circuits. Adding the initial 1 from A to A 1 gives us that 1 + 2 R 1 1 + 1 = R . Solving this equation, R = 2 .
Please colud you explain your solution again and briefly , and i don't even understant what is A1 in your solution. :(
We can add two 2 ohm resistances on front and resultant resistance must be 2R. Solving the eqn we get R=√2 ohm.