Infinite Reuleaux Hypnosis

Geometry Level 3

The largest green Reuleaux Triangle is regular and has area as 5 unit². The largest red Reuleaux Triangle is the one that whose equilateral triangle is made by joining the midpoint of the largest green Reuleaux Triangle's interior equilateral triangle. Similarly the pattern continues to infinity. Find sum areas of the green region.


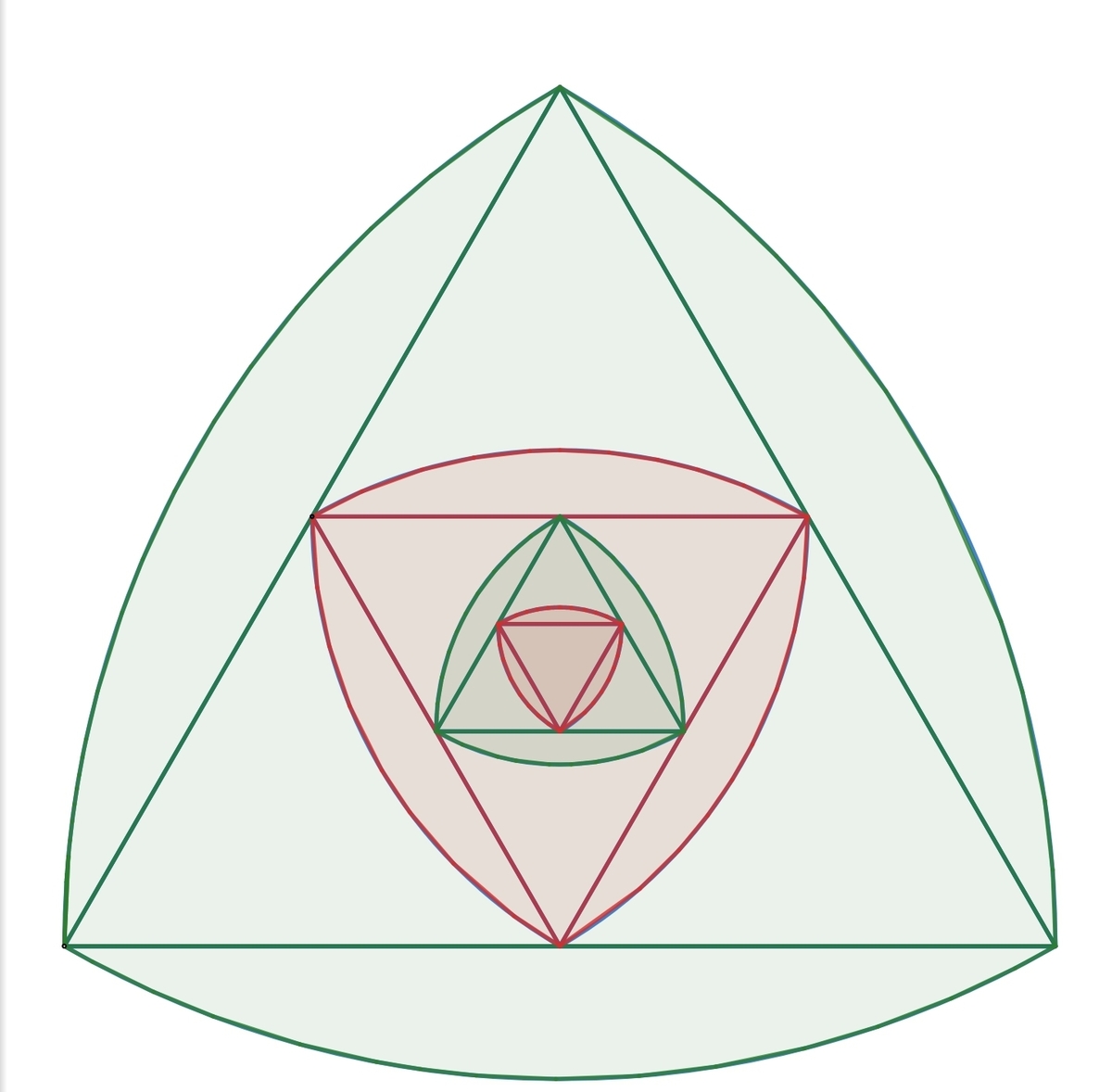
The answer is 4.

Omek K by Omek K , 15, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Lu Ca
May 4, 2021

Each outer green zone is 4 time the inner adjacent red area, hence the green area fraction is 4 4 + 1 = 4 5 \frac{4}{4+1} = \frac{4}{5} so, if the largest green Reuleaux Triangle has area as 5 unit², then the green zone has in total 5 ⋅ 4 4 + 1 = 4 5 \cdot \frac{4}{4+1} = 4 unit²

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Saya Suka
Apr 30, 2021

1st green – 1st red
= 5 – (1/2)² × 5
= 5 × (1 – 1/4)
= 15 / 4


To the infinity and 'beyond'
= a / (1 – r)
= ( 15 / 4 ) / ( 1 – ( (1/2) × (1/2) )² )
= ( 15 / 4 ) × ( 16 / 15 )
= 16 ÷ 4
= 4

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...