Infinite Roots
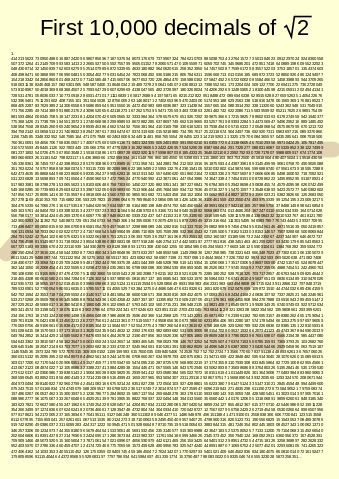
What is 2 0 + 2 0 + 2 0 + . . . . ? Write your answer as as a + b , where b a is equal to 2 0 + 2 0 + 2 0 + . . . . , and a and b are relatively prime
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Mine is a similar solution
That moment when you want to make your solution look different so you use 3 \boxed{} xD
Let's take,
2 0 + 2 0 + 2 0 + . . . . = x
We can also write it as,
2 0 + x = x 2 0 + x = x 2 x 2 − x − 2 0 = 0 x 2 − 5 x + 4 x − 2 0 = 0 x ( x − 5 ) + 4 ( x − 5 ) = 0 ( x − 5 ) ( x + 4 ) = 0
Therefore, the roots of the equation are, x = 5 and x = − 4 . As the second result is negative we can ignore it, So, the solution is 5 , or 1 5
And hence, a + b = 5 + 1 = 6
This looks exactly like @Sravanth Chebrolu 's solution above.
Log in to reply
Yeah, looks like he copied it.(see the dates)
Log in to reply
Yeah i saw that before I posted my earlier comment.
YES!! Jonathan, you can finally use L A T E X ! Solution: b a is equal to 1 5 , so a + b is equal to 5 + 1 or 6
Please explain how you got your answer.
As Sravanth Chebrolu has explained, the value is 5 . But do not forget that the question is asking for fraction form so the answer is NOT 5 . We assume the denominator to be 1 since we have a whole number so a + b = 5 + 1 = 6 .
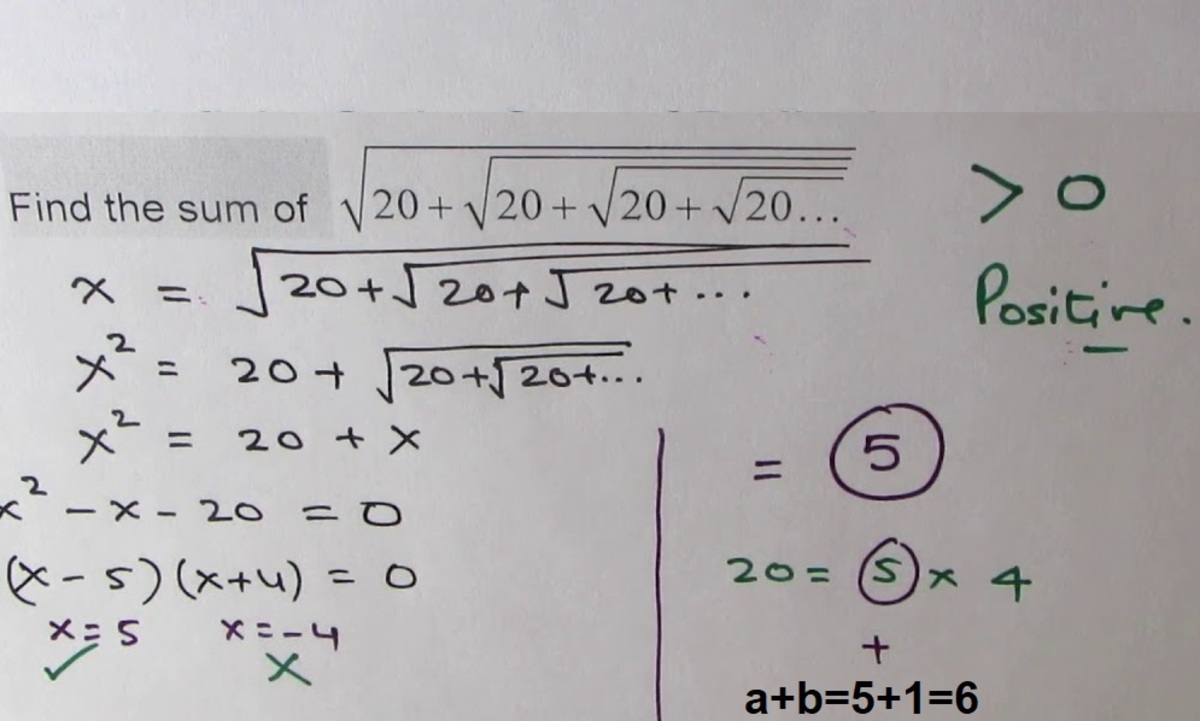
Let's take, 2 0 + 2 0 + 2 0 + . . . . = x
We can also write it as, 2 0 + x = x 2 0 + x = x 2 x 2 − x − 2 0 = 0 x 2 − 5 x + 4 x − 2 0 = 0 x ( x − 5 ) + 4 ( x − 5 ) = 0 ( x − 5 ) ( x + 4 ) = 0
Therefore, the roots of the equation are, x = 5 and x = − 4 . As the second result is negative we can ignore it, So, the solution is 5 , or 1 5
And hence, a + b = 5 + 1 = 6