Infinite Series (Problem 1)
Find the sum below.
n = 0 ∑ ∞ 3 ( n + 1 ) ( n + 3 ) 4 π
The answer is 3.1415.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Karan Chatrath , can you please add the steps involving in integrating the function and fully show how did you get π from the second part of your boxed final answer? It will be beneficial to me and everybody who attempts this question.
Dude ,that's a hell of a solution well you can make the argument more elegant by using the Digamma function.Try Brilliant website for more details.
The given expression is equal to
3 2 π ( n = 0 ∑ ∞ ( n + 1 1 − n + 3 1 ) ) .
This telescopic sum reduces to 3 2 π × 2 3 = π ≈ 3 . 1 4 1 5 9 .
Alak Bhattacherya both the sums diverges if you calculated them separately.Please use a single sigma notation with brackets surrounding the inner input.
Hi Mr. Alak, can you please elaborate on how you got the telescopic sum to be 2 3 ?
Log in to reply
k = 0 ∑ n n + 1 1 − n + 3 1 = k = 1 ∑ n + 1 n 1 − k = 3 ∑ n + 3 n 1 = 1 + 2 1 − n + 2 1 − n + 3 1
Then let n goes to ∞ .
S = n = 0 ∑ ∞ 3 ( n + 1 ) ( n + 3 ) 4 π = 3 4 π n = 1 ∑ ∞ n ( n + 2 ) 1 = 3 2 π n = 1 ∑ ∞ ( n 1 − n + 2 1 ) = 3 2 π ( 1 1 + 2 1 ) = π ≈ 3 . 1 4 2
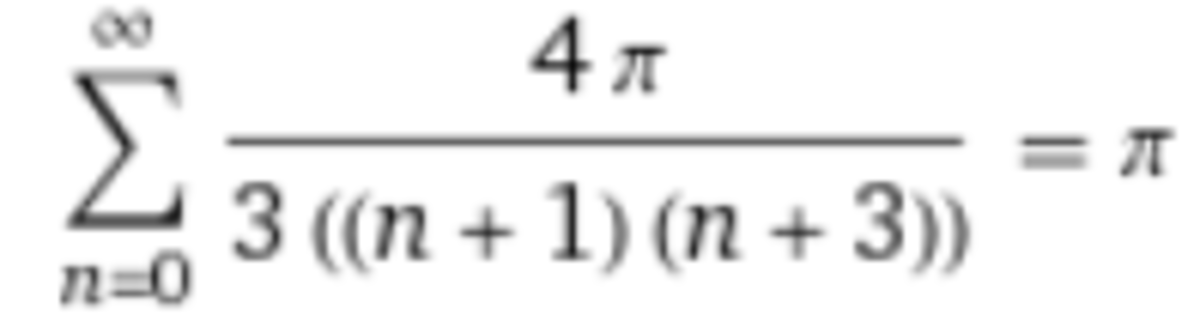
The first 5 digits of π only are needed
Therefore, the answer is 3 . 1 4 1 5 ≈ π .
Consider the infinite series for all ∣ x ∣ < 1 :
1 − x 1 = n = 0 ∑ ∞ x n
Integrating both sides from 0 to y :
− ln ( 1 − y ) = n = 0 ∑ ∞ n + 1 y n + 1
Multiplying both sides by y :
− y ln ( 1 − y ) = n = 0 ∑ ∞ n + 1 y n + 2
Integrating both sides from 0 to 1 gives:
− ∫ 0 1 y ln ( 1 − y ) d y = n = 0 ∑ ∞ ( n + 1 ) ( n + 3 ) 1
Multiplying both sides by 3 4 π :
− 3 4 π ∫ 0 1 y ln ( 1 − y ) d y = n = 0 ∑ ∞ 3 ( n + 1 ) ( n + 3 ) 4 π
The steps required to evaluate the integral are provided below. The required answer is:
n = 0 ∑ ∞ 3 ( n + 1 ) ( n + 3 ) 4 π = − 3 4 π ∫ 0 1 y ln ( 1 − y ) d y = π
Consider the indefinite integral:
I = − ∫ y ln ( 1 − y ) d y
Integrating by parts:
I = − 2 y 2 ln ( 1 − y ) − ∫ 2 ( 1 − y ) y 2 d y I = − 2 y 2 ln ( 1 − y ) + ∫ 2 ( 1 − y ) 1 − y 2 − 1 d y I = − 2 y 2 ln ( 1 − y ) + ∫ 2 1 + y d y − ∫ 2 ( 1 − y ) 1 d y I = − 2 y 2 ln ( 1 − y ) + 2 y + 4 y 2 + 2 ln ( 1 − y ) I = 2 ( 1 − y 2 ) ln ( 1 − y ) + 2 y + 4 y 2
Now consider the definite integral:
− ∫ 0 a y ln ( 1 − y ) d y = 2 ( 1 − a 2 ) ln ( 1 − a ) + 2 a + 4 a 2
− a → 1 − lim ∫ 0 a y ln ( 1 − y ) d y = a → 1 − lim ( 2 ( 1 − a 2 ) ln ( 1 − a ) + 2 a + 4 a 2 ) − ∫ 0 1 y ln ( 1 − y ) d y = a → 1 − lim ( 2 ( 1 − a 2 ) ln ( 1 − a ) ) + 4 3
The only limit on the right-hand side can be evaluated as such:
a → 1 − lim 2 ( 1 − a 2 ) ln ( 1 − a ) = a → 1 − lim 1 − a 2 2 ln ( 1 − a )
Beyond this, point L'hopital's rule can be applied to prove that the above limit evaluates to zero.
Therefore: − ∫ 0 1 y ln ( 1 − y ) d y = 4 3