Infinite Square Root

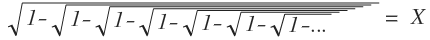
You just square both sides and you get

$1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-... } } } } } } } =\quad { X }^{ 2 }$

then you can substitute the value of $\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-\sqrt { 1-... } } } } } } }$ with $X$ since they are equal

your equation right now will become $1-X={ X }^{ 2 }$ , by this equation you can get the value of the $X$ and that would be $0.618$

To solve this question, we will take an assumption.

Let: $x=\sqrt{1-\sqrt{1-\sqrt{1-......}}}$

$x=\sqrt{1-x}$

Squaring both sides, we get:

$x^{2}=1-x$

$x^{2}+x-1=0$

Using quadratic equation:

$=\frac{-b+-\sqrt{b^{2}-4ac}}{2a}$

$=\frac{-1+-\sqrt{1^{2}-4\times1\times(-1)}}{2\times1}$

$=\frac{-1+-\sqrt{1+4}}{2}$

$=\frac{-1+-\sqrt{5}}{2}$

$x=\frac{-1+\sqrt{5}}{2},\frac{-1-\sqrt{5}}{2}$

$x=0.618,-1.618$ (Both values are approx.)

Since, $x$ is not taken as negative.

Thus, the answer is: $x=\boxed{0.618}$