Infinite towers of some familiar constants
Among the following infinite tetrations of numbers given, how many of them converge to a particular value?
(A) e e e ⋅ ⋅ ⋅
(B) 5 5 5 ⋅ ⋅ ⋅
(C) 2 2 2 ⋅ ⋅ ⋅
(D) 3 3 3 ⋅ ⋅ ⋅
(E) φ φ φ ⋅ ⋅ ⋅
(F) π π π ⋅ ⋅ ⋅
(G) e e e ⋅ ⋅ ⋅
(H) π π π ⋅ ⋅ ⋅
(I) φ φ φ ⋅ ⋅ ⋅
(J) γ γ γ ⋅ ⋅ ⋅
(K) γ γ γ ⋅ ⋅ ⋅
About some of the above mentioned constants:
- e ≈ 2 . 7 1 8 2 8 . . . , denotes the Euler's number .
- π ≈ 3 . 1 4 1 5 9 . . . , called as ' pi ' denotes the ratio of the circumference of a circle to its diameter.
- φ = 2 1 + 5 ≈ 1 . 6 1 8 0 3 . . . , denotes the Golden Ratio .
- γ ≈ 0 . 5 7 7 2 1 . . . , denotes the Euler Mascheroni constant .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Are you sure they converge to a particular value and not to more than one value??
Log in to reply
As a limit, within the range of values as already noted, there's only one value. That is, if you start with x 1 , and then find x 2 = x 1 x 1 to then find x 3 = x 1 x 2 , etc., it'll converge to a single limit, and there is no confusion. Otherwise, why, yes, there's "another value". Let me go see if I can find that graph.
Here it is, showing how x = 2 "can have more than one value"
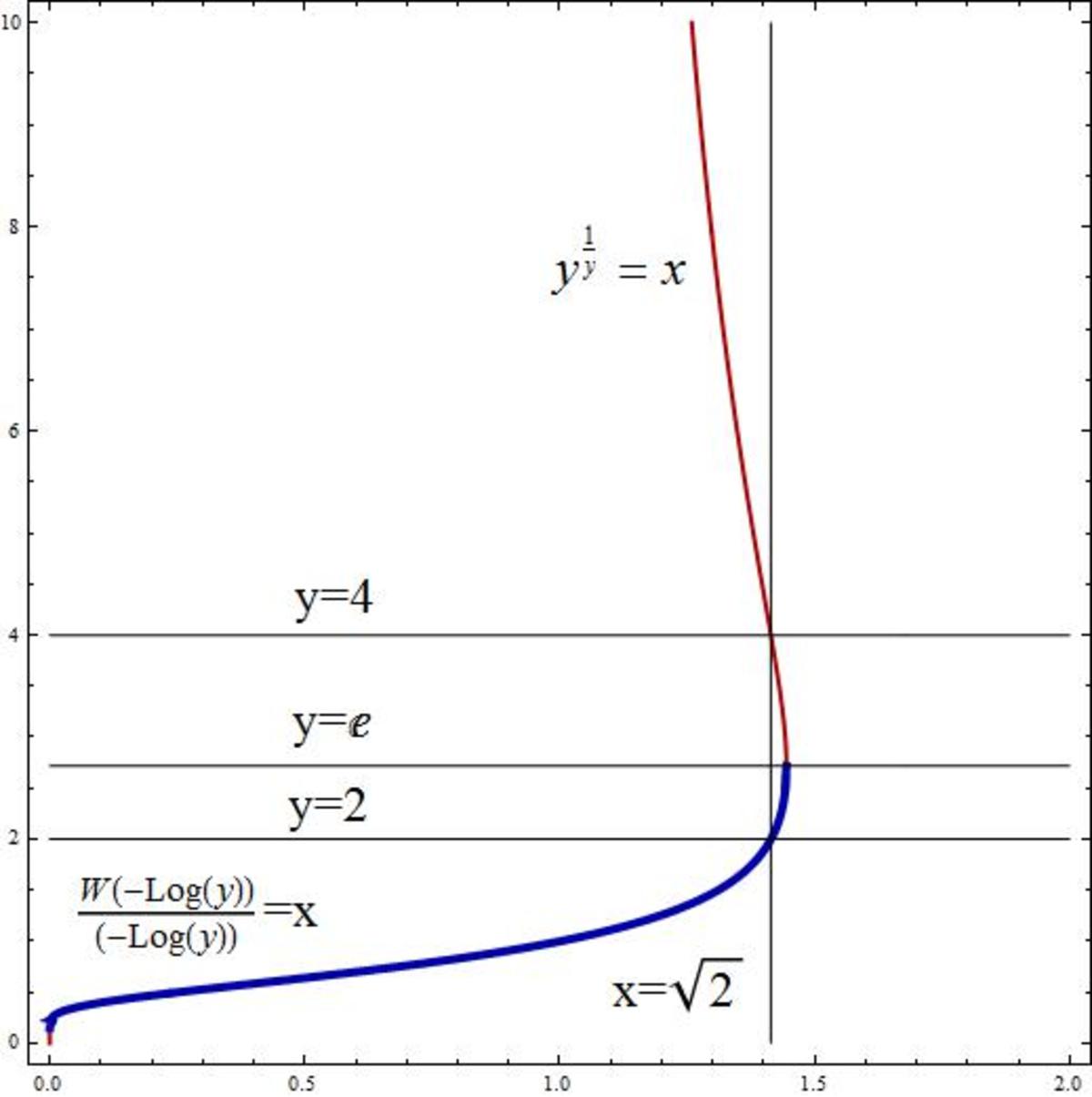
And then there's that special range x = 0 to x = e − e where the function actually sort of bifurcates, i.e., jumps from one curve to another as the iteration is being done.
This infinite tetration is well defined only for the range of values from e − e to e e 1 , or about 0 . 0 6 5 9 8 . . . to 1 . 4 4 4 6 7 . . . . Check which ones from A to K falls in this range. A does not, for example.