Infinite triangular Resistance
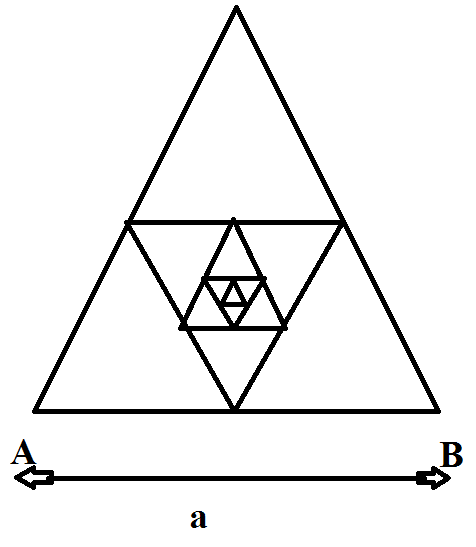
Determine the resistance between the points A and B of the frame made of thin homogeneous wire (as shown in figure), assuming that the number of successively embedded equilateral triangles (with sides decreasing by half) tends to infinity. Side is equal to units and the resistance of unit length of wire is units.
If the resistance is of the form , find .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I t f o l l o w s f r o m t h e s y m m e t r y c o n s i d e r a t i o n s t h a t t h e i n i t i a l c i r c u i t c a n b e r e p l a c e d b y a n e q u i v a l e n t o n e a s s h o w n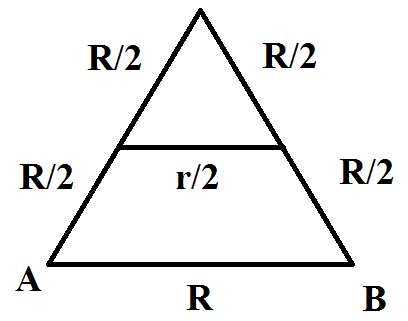 W
e
r
e
p
l
a
c
e
t
h
e
i
n
n
e
r
t
r
i
a
n
g
l
e
c
o
n
s
i
s
t
i
n
g
o
f
a
n
i
n
f
i
n
i
t
e
n
u
m
b
e
r
o
f
e
l
e
m
e
n
t
s
b
y
a
r
e
s
i
s
t
o
r
o
f
r
e
s
i
s
t
a
n
c
e
2
R
A
B
,
w
h
e
r
e
t
h
e
r
e
s
i
s
t
a
n
c
e
R
A
B
i
s
s
u
c
h
t
h
a
t
R
A
B
=
r
=
a
ρ
,
a
f
t
e
r
s
i
m
p
l
i
f
i
c
a
t
i
o
n
,
t
h
e
c
i
r
c
u
i
t
b
e
c
o
m
e
a
s
y
s
t
e
m
o
f
s
e
r
i
e
s
a
n
d
p
a
r
a
l
l
e
l
r
e
s
i
s
t
a
n
c
e
s
.
I
n
o
r
d
e
r
t
o
f
i
n
d
r
i
w
r
i
t
e
t
h
e
e
q
u
a
t
i
o
n
r
=
R
(
R
+
R
+
2
r
R
.
2
r
)
(
R
+
R
+
R
+
2
r
R
.
2
r
)
−
1
s
o
l
v
i
n
g
a
b
o
v
e
e
q
u
a
t
i
o
n
r
=
a
ρ
(
3
7
−
1
)
W
e
r
e
p
l
a
c
e
t
h
e
i
n
n
e
r
t
r
i
a
n
g
l
e
c
o
n
s
i
s
t
i
n
g
o
f
a
n
i
n
f
i
n
i
t
e
n
u
m
b
e
r
o
f
e
l
e
m
e
n
t
s
b
y
a
r
e
s
i
s
t
o
r
o
f
r
e
s
i
s
t
a
n
c
e
2
R
A
B
,
w
h
e
r
e
t
h
e
r
e
s
i
s
t
a
n
c
e
R
A
B
i
s
s
u
c
h
t
h
a
t
R
A
B
=
r
=
a
ρ
,
a
f
t
e
r
s
i
m
p
l
i
f
i
c
a
t
i
o
n
,
t
h
e
c
i
r
c
u
i
t
b
e
c
o
m
e
a
s
y
s
t
e
m
o
f
s
e
r
i
e
s
a
n
d
p
a
r
a
l
l
e
l
r
e
s
i
s
t
a
n
c
e
s
.
I
n
o
r
d
e
r
t
o
f
i
n
d
r
i
w
r
i
t
e
t
h
e
e
q
u
a
t
i
o
n
r
=
R
(
R
+
R
+
2
r
R
.
2
r
)
(
R
+
R
+
R
+
2
r
R
.
2
r
)
−
1
s
o
l
v
i
n
g
a
b
o
v
e
e
q
u
a
t
i
o
n
r
=
a
ρ
(
3
7
−
1
)