Infinite Volume Or Finite Volume?

Calculus Level 4

Rotate the curve drawn by the function f ( x ) = x − a f(x)=x^{-a} , a a a positive real number, for x > 1 x>1 , about the x x -axis, as so:

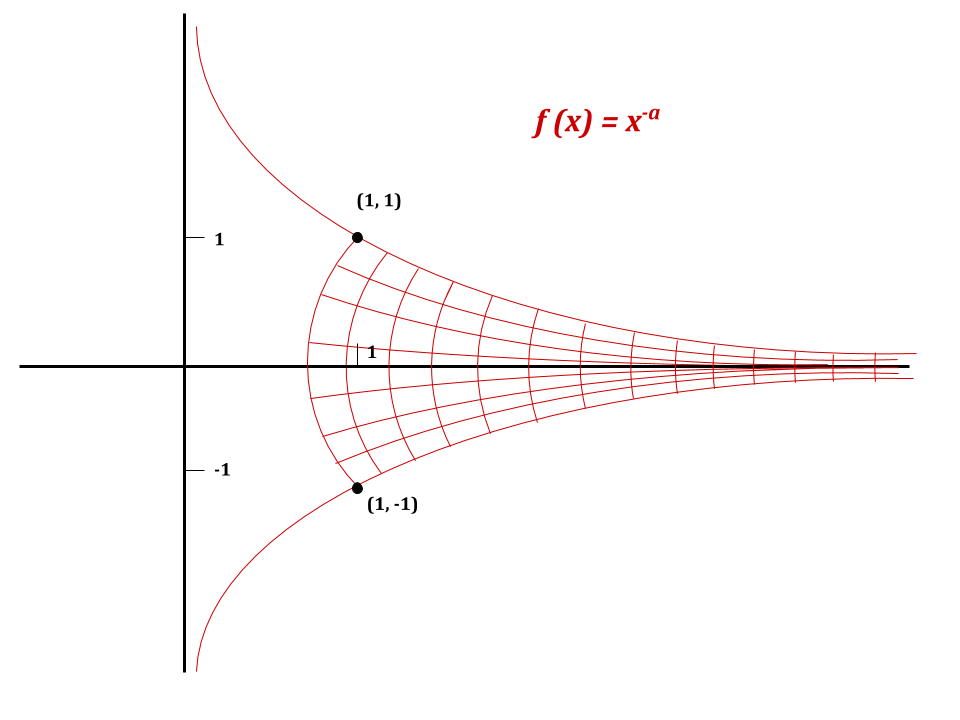
For which values of a a is the volume of the resulting solid finite?

Bonus: For the correct inequality, what is the volume in terms of a a ?

a > 1 a>1 a > 0 a>0 a ≥ 1 a\geq1 a > 1 2 a>\frac{1}{2} a ≥ 1 2 a\geq\frac{1}{2}

Andrei Li by Andrei Li , 16, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Andrei Li
Aug 17, 2018

The area can be expressed as the area of an infinite number of discs, with 'height' Δ x \Delta x , 'radius' x − a = 1 x a x^{-a}=\frac{1}{x^a} , and 'area' π x − 2 a Δ x \pi x^{-2a} \Delta x . As Δ x → 0 \Delta x \to 0 , the limit is the improper integral

lim ⁡ x → ∞ π ∫ 1 ∞ x − 2 a d x \lim_{x\to\infty} \pi \int_1^{\infty} x^{-2a} dx

Using the power rule for integration, the integral becomes

∫ x − 2 a d x = x 1 − 2 a 1 − 2 a = 1 ( 1 − 2 a ) x 2 a − 1 \int x^{-2a} dx = \frac{x^{1-2a}}{1-2a}= \frac{1}{(1-2a)x^{2a-1}}

When x = 1 x=1 , this is π 1 − 2 a \frac{\pi}{1-2a} . Now, in order for the volume to be finite, lim ⁡ x → ∞ 1 ( 1 − 2 a ) x 2 a − 1 \lim_{x\to\infty}\frac{1}{(1-2a)x^{2a-1}} must be equal to 0 0 , or

lim ⁡ x → ∞ ( 1 − 2 a ) x 2 a − 1 = ∞ \lim_{x\to\infty}(1-2a)x^{2a-1}=\infty

In order for that to occur, the exponent of x x must be greater than 0 0 .

2 a − 1 > 0 ⟹ a > 1 2 2a-1>0\implies a>\frac{1}{2}

Thus, a > 1 2 a>\frac{1}{2} . Now, if this condition is satisfied,

lim ⁡ x → ∞ π ∫ 1 ∞ x − 2 a d x = − π 1 − 2 a = π 2 a − 1 \lim_{x\to\infty} \pi \int_1^{\infty} x^{-2a} dx=-\frac{\pi}{1-2a}=\frac{\pi}{2a-1}

5 Helpful 0 Interesting 0 Brilliant 0 Confused

Didn't they say x > 1, meaning it's safe to include a = 1/2

John Morcos - 2 years, 9 months ago

Log in to reply

Inputting a = 1 2 a=\frac{1}{2} into 1 ( 1 − 2 a ) x 2 a − 1 \frac{1}{(1-2a)x^{2a-1}} gives 1 0 \frac{1}{0} , which is clearly not defined.

Andrei Li - 2 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...