Infinitely Infinite Resistors
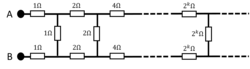 Find the resistance between the points
A
and
B
of an infinite circuit shown. The resistance of the resistors in each loop is twice those of the previous loop on its left.
Find the resistance between the points
A
and
B
of an infinite circuit shown. The resistance of the resistors in each loop is twice those of the previous loop on its left.
Given that the resistance can be written as:
c a + b
Find a + b + c
SJPO SPECIAL ROUND 2010
This question is part of my set SJPO Practice Questions
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
This is a beautiful solution. The coarse graining cuts through some needless algebra.
I see now that there is a misprint in the calculation by Chew Seong Cheong, the 8 for c should be a 4!
The resistance of the circuit can be written as an infinite fraction:
2 ( 2 0 ) + 2 0 1 + 2 ( 2 1 ) + 2 1 1 + 2 ( 2 2 ) + . . . 1 1 1 1 1 = 2 1 + 2 0 1 + 2 2 + 2 1 1 + 2 3 + . . . 1 1 1 1 1 = x − − − ( 1 )
And so,
2 x = 2 2 + 2 1 1 + 2 3 + 2 2 1 + 2 4 + . . . 1 1 1 1 1 − − − ( 2 )
This makes:
( 2 ) s u b s t i t u t e i n t o ( 1 ) : x = 2 1 + 2 0 1 + 2 2 + 2 1 1 + 2 3 + . . . 1 1 1 1 1 = 2 + 1 + 2 x 1 1
Solving for:
x = 2 + 1 + 2 x 1 1
Gives:
x = 4 5 ± 4 1
Since
x > 2
x = 4 5 + 4 1 = c a + b
Making a + b + c = 5 0
For each loop, resistance becomes 2 times. So, if equivalent resistance between A and B is x, then the equivalent resistance of second loop is 2x. Now 2x and 1 in parallel and this is in series with the two 1,s. This is equal to x(equivalent resistance between A and B). This gives us a quadratic in x, (x^2 - 5x - 2 =0). On solving, we get a=5, b=41, c=4. So, a+b+c=50
I know where that came from......he he
Log in to reply
Gud you know
are you by any chance PANJ sirs student
Let the equivalent resistance be R . Since the circuit is infinite, we have (see diagram below):
R ⇒ R ( 1 + 2 R ) R + 2 R 2 2 R 2 − 5 R − 2 ⇒ R ⇒ a + b + c = 1 + 1 ∣ ∣ 2 R + 1 = 2 + 1 + 2 R 1 × 2 R = 2 ( 1 + 2 R ) + 2 R = 2 + 6 R = 0 = 8 5 + 2 5 + 1 6 = 8 5 + 4 1 = 5 + 4 1 + 8 = 5 0