Infinite Infinities
2 n = 0 ∑ ∞ ⎣ ⎢ ⎢ ⎢ ⎡ 2 ⎣ ⎢ ⎢ ⎢ ⎡ 2 0 1 3 2 ∑ n = 0 ∞ [ 2 [ 2 0 1 3 2 ∑ n = 0 ∞ [ 2 [ 2 0 1 3 . . . ] n ] − 1 ] n ] − 1 ⎦ ⎥ ⎥ ⎥ ⎤ n ⎦ ⎥ ⎥ ⎥ ⎤ − 1
What is the value of the nested summation above?
This might look daunting at first but the solution will come out very nicely and easily.
The answer is 2014.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Though the answer comes out correct, their is a mistake towards the end of the solution where 2013 should also be raised to the power n:
∑ n = 0 ∞ x n 2 0 1 3 n = x
Since this goes on for infinity, this can be written as:
2 ∑ n = 0 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = x
Now let:
2 ∑ n = 0 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = S
∑ n = 0 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = 2 S
∑ n = 1 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = 2 S [ 2 0 1 3 x ] 1 ∴ ∑ n = 0 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 − ∑ n = 1 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = [ 2 [ 2 0 1 3 x ] 0 ] − 1 = 2 1 = 2 S − 2 S [ 2 0 1 3 x ] 1 = 2 x S x − 2 0 1 3 S
Solving for S gives: S = x − 2 0 1 3 x
And since 2 ∑ n = 0 ∞ [ 2 [ 2 0 1 3 x ] n ] − 1 = x , x − 2 0 1 3 x = x
Solving for x gives x = 2 0 1 4 o r 0
Since x > 0 , x = 2 0 1 4
By the way, can anyone tell me what this method is called?
Call it Poonisation.
I just applied the infinite g.p. formula after putting in x in first step.
Log in to reply
Actually, this is deriving infinite g.p, so its the same thing actually.
I solved it in similar way , nut don't know what it is called .
One of my teacher calls it infinite resistance. Since its similar to the way we solve resistors connected up to infinity
I have written the solution on a paper. Please see the image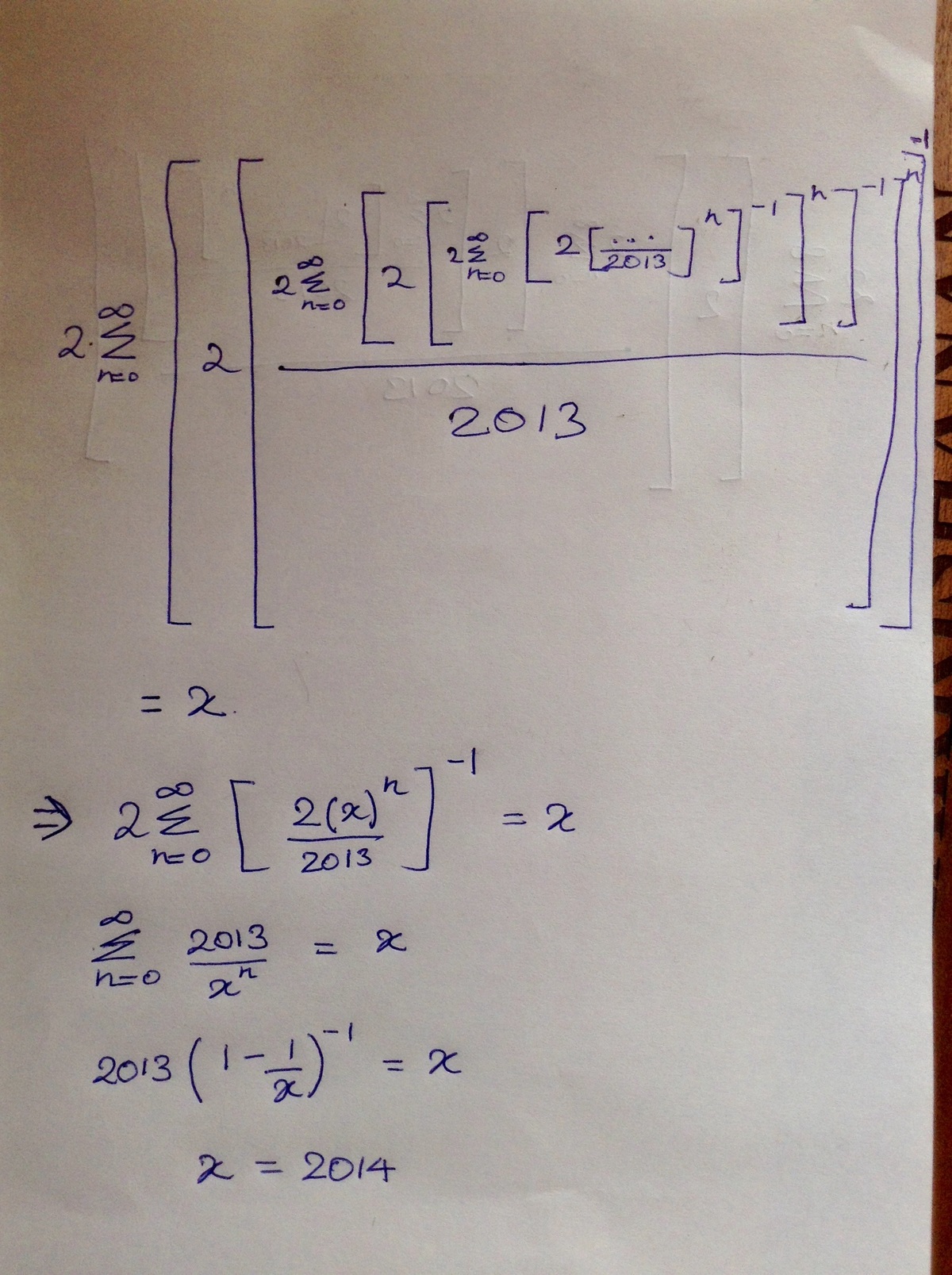 .
.