Prime Exponents Tower
What is the last digit when this exponent tower of primes is expanded?
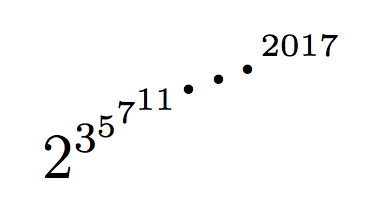
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The number 5 is odd, as is 5 m for any natural number m . Hence 3 5 m ≡ 3 ( mod 4 ) , and therefore 2 3 5 m ≡ 2 3 ≡ 8 ( mod 1 0 ) .
How do you know 3 5 m must be 3(mod 4) and it can't be 1(mod 4)?
Log in to reply
Because the exponent 5 m is odd. 3 2 k + 1 = 3 2 k ⋅ 3 = 9 k ⋅ 3 ≡ 1 k ⋅ 3 ≡ 3 ( m o d 4 ) .
Log in to reply
why can't we see it as 5*m in place of 5^m
Hey, i am unfamiliar with this cocept of writing (mod x). Would you please guide me here
Log in to reply
https://brilliant.org/math-formatting-guide/
Had the same problem. I have found an answer here . "a = b (mod n) means that n is a divisor of a - b"
5^(anything) has last digit 5
3^(5) or 3^(25) ... has last digit 3
2^(multiple of 3 having last digit 3) = 8
solution by: Sushil Verma
Consider the sequence of remainders when 2 n is divided by 10. For n = 1 , 2 , 3 , … , we obtain 2 , 4 , 8 , 6 , 2 , 4 , 8 , 6 , … . The pattern repeats every 4 terms. So we want to discover what is the remainder of 3 5 … when divided by 4.
Consider the sequence of remainders when 3 n is divided by 4. For n = 1 , 2 , 3 , … , we obtain 3 , 1 , 3 , 1 , 3 , 1 , … . The pattern repeats ever 2 terms. So we want to discover what is the remainder of 5 7 … when divided by 2.
The number 5 is odd, so 5 n is always going to be odd.
Hence 3 5 … is going to leave a remainder of 3 when divided by 4.
Hence 2 3 5 … is going to leave a remainder of 8 when divided by 10. Thus, the last digit is 8.